Нехай задане комплексне число z=a+b*i, яке на координатній площині можна відобразити у вигляді точки A чи вектора OA .
Позначимо - кут, який утворює промінь OA з додатним напрямком осі , а через OA=r - довжину променя. Тоді справедливі наступні закономірності
- модуль комплексного числа z;
- аргумент комплексного числа z.
Модулем комплексного числа z називається його довжина в декартовій системі координат, яка визначається за формулою
Аргумент комплексного числа z визначається так: 
де кут 
- визначають із системи рівнянь:
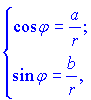
і він належить проміжку [0; 2*Pi].
Для визначення чверті, в якій знаходиться кут, використовують наступні правила
чверть: 
чверть: 
чверть: 
чверть: 
Коли 
кут приймає значення
коли 
і
у випадках 
При 
кут приймає значення
коли 
і
у випадках 
Запам'ятайте як знаходити кут, це Вам потрібно в першу чергу для обчислень, з іншої сторони підтягнете знання з тригонометрії.
Очевидно, що будь-який розв'язок 
системи рівнянь має вигляд 
Тригонометрична форма комплексного числа
Коротко - це число записане через радіус вектор та кут за форулою
Два комплексних числа, задані у тригонометричній формі називаються рівними між собою тоді і тільки тоді, коли їх модулі рівні, а аргументи або рівні, або відрізняються на період 
Розглянемо іька прикладів, щоб закріпити теоретичний матеріал.
Приклад 1. Знайти модуль і аргумент комплексного числа
1) 
2) 
3) 
Розв'язок. Уважно розгляньте та вивчіть схеми наступних перетворень з комплексними числами
1) Знайдемо модуль комплексного числа. Для цього сумуємо квадрати дійсної та уявної чатини числа, після чого добуваємо корінь квадратний
Кут належить ІV чверті, оскільки a>0, b<0. Знайдемо його значення через тангенс
Отже, задане комплексне число буде мати наступні модуль і аргумент 
2) Обчислюємо модуль комплексного числа 
згідно правила 
Кут 
знаходиться в третій чверті, оскільки a<0, b<0. Знайдемо його значення через синус
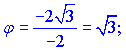
Заданому комплексному числу має відповідають наступні модуль та аргументу
3) Модуль числа знаходимо за формулою
Кут 
знаходиться в першій чверті, оскільки a>0, b>0.
Його значення обчислюємо через тангенс
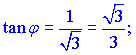
Шукані величини приймуть значення
При обчисленнях аргумента комплексного числа через тангенс звертайте увагу на чверть в якій знаходиться кут. Неврахування цього часто приводить до помилок. Обчислення модуля, як правило, простіше і не вимагає особливих знань при вивченні даної теми. Також вивчіть таблицю синусі та осинусів кутів, або хоча б роздрукуйте, щоб мати перед очима при знаходженні аргумену омплексного числа.
