Комплексні рівняння виду Zk-Z0=0 найчастіше задають студентам на контрольних, тестах, зрізах для перевірки вмінь застосовувати правило Муавра та при обчисленні коренів будь-якого степеня з комплексного числа.
Нехай задана число z0 в комплексній площині чи дійсній, завдання полягає в знаходженні коренів n-го степеня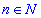 
(коренів рівняння zn=z0 ) . Запишемо числа z, z0 в тригонометричній формі
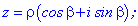
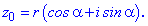
Формула Муавра-Лапласа
За формулою Муавра, маємо наступну залежність між ними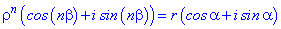
З рівності модулів матимемо матимемо формулу для модулів
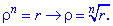Подібним чином формула Муавра зв'язує аргументи комплексних чисел
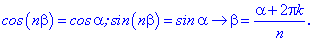Остаточно, корені рівняння будуть мати вигляд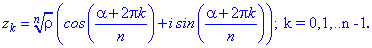
Це і є формула Муавра, яку часто називають формулою Муавра-Лапласа.
При більших значеннях лічильника k=n, ... корені просто будуть повторюватися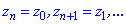
тому параметр змінюється в діапазоні k= 0,..,n-1.
Самі ж корені, а віврніше їх аргументи лежать на колі одиничного радіусу. Достатньо тільки знайти перший, а всі решта отримаємо додаванням кута 2Pi/n.
Розв'яжемо популярні для студентів приклади на відшукання коренів.
Приклад 1. Знайти корені рівняння z3-1=0.
Розв'язання. Перепишемо рівняння у вигляді z3=1 та представимо 1 в тригонометричній формі
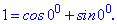
Наступним кроком застосовуємо формулу Муавра
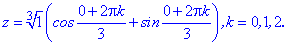
Підстановкою значень k=0,1,2 знаходимо три корені рівняння.
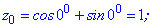
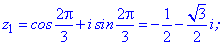
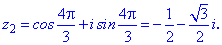
Для спрощення подібних обчислень складемо розрахункову програму в Maple для обчислення і графічної побудови аргументів коренів.
Знаходження коренів комплекного числа в Maple
Для початку обнулимо всі змінні і підключимо пакет роботи з графікою.
> restart;with(plots):
Далі зробимо програмний код універсальним. Для цього для кожного рівняння нам потрібно буде задати лише дійсну частину (a), уявну частину (b) комплексного числа, та корінь якого степеня потрібно знайти (k).
> a:=1; b:=0; k:=3;
Обчислюємо модулі комплексних чисел
> R:=sqrt(a^2+b^2);
> rho=R^(1/k);
Дальше обчислюємо значення аргументу в градусах першого кореня
> alpha:=evalf(arccos(a/R))/3.14*180;
Наступним кроком в циклі обчислюємо корені рівняння, та окремо значення косинусів та синусів кутів.
> for i from 0 to k-1 do
z[i]:=rho*(cos((alpha+2*Pi*i)/k)+I*sin((alpha+2*Pi*i)/k));
x[i]:=cos((alpha+2*Pi*i)/k);
y[i]:=sin((alpha+2*Pi*i)/k) end do;
На основі обчислень, коренями попереднього завдання будуть значення
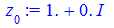
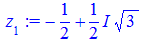
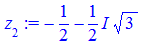
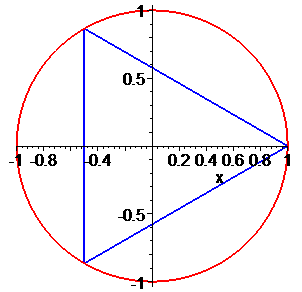
Дальше записуємо код, який відповідає за графічний вивід одиничного кола та многокутника, вершинами якого будуть аргументи коренів. При рівнянні третього порядку отримаємо рівносторонній трикутник, четвертого порядку – квадрат, далі п'ятикутник, шестикутник і т.д.
> Q1:=plot(sqrt(1-x^2), x=-1..1,thickness=2): Q2:=plot(-sqrt(1-x^2), x=-1..1,thickness=2): Q3:=plot([seq([x[m],y[m]],m=0..k-1), [x[0],y[0]]],color=blue,thickness=2):
> display(Q1,Q2,Q3);
Значення аргументів добре ілюструє наступний рисунок. Многокутник відповідає сполученню коренів рівняння.
При необхідності знайдені корені можна округлити
> for i from 0 to k-1 do Z[i]:=evalf(z[i]) end do;
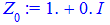
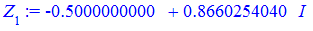
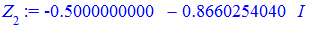
Ось і вся музика.
Приклад 2. Знайти корені рівняння z4+625=0.
Розв'язання. Запишемо рівняння у вигляді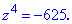 
Число в правій стороні рівності (-625) подаємо в тригонометричній формі
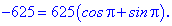
За формулою Муавра корені шукаємо за формулою
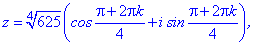
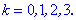
Перебором можливих значень лічильника 0-3 отримаємо
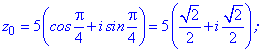
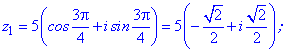
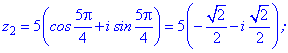
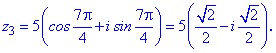
На цьому приклад розв'язано!
Хто має можливість мое вMaple виконуємо перевірку та побудову розв'язків
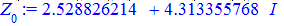
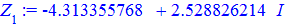
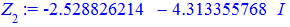
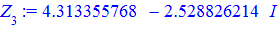
Приклад 3. Розв'язати рівняння z5=1.
Розв'язання. Представимо одиницю в тригонометричній формі
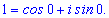
Використовуючи формулу Муавра знаходимо п'ять коренів. Аргументи будуть відрізнятися між собою на кут 2Pi/5=72 градуси
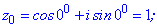
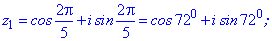
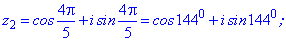
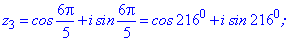
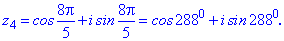
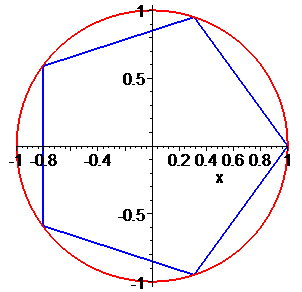
Остаточні значення (з паваючою крапкою) та многокутник отримаємо розрахунками в Maple
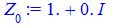
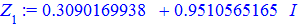
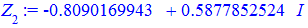
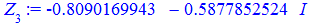
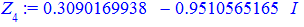
Квадратне рівняння з комплексними коефіцієнтами
Приклад 4. Розв'язати квадратне рівняння з комплексними коефіцієнтами.
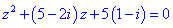
Розв'язання. Розв'язуємо за стандартною схемою для квадратного рівняння. Знаходимо дискримінант рівняння
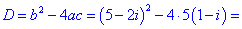
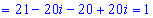
На щастя він приймає дійсне значення – це спрощує обчислення. Знаходимо корені рівняння
;
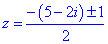
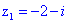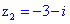
Досить легке в плані розрахунків завдання.
Приклад 5. Розв'язати квадратне рівняння
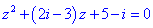
Розв'язання. Обчислюємо дискримінант квадратного рівняння.
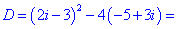
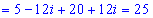
Дальше визначаємо корені за формулою
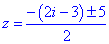
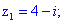
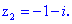
Тут теж повезло з дискримінантом - він виявився дійсним числом.
Приклад 6. Розв'язати комплексне рівняння
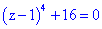
Розв'язання. Хтось подумає "чому комплексне?"
Зараз ми це перевіримо
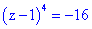
Дійсно комплексне, записуємо константу в тригонометричній формі
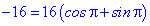
Корені рівняння знаходимо із формули Муавра-Лапласа
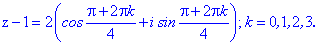
Для кожного із рівнянь отримаємо відповідний розв'язок
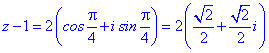
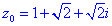
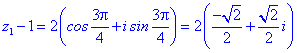
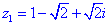
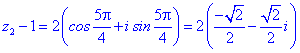
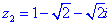
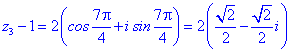
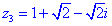
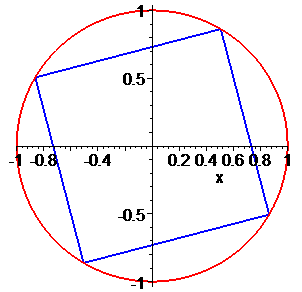
Всі 4 корені належать колу, перший має аргумент 45 градусів, решта 3 зміщені на прямий кут.
Приклад 7. Розв'язати рівняння
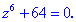
Розв'язання. Тригонометрична форма -64 буде наступною
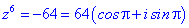
Застосовуємо формулу Муавра для обчислення коренів
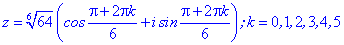
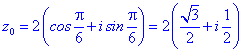
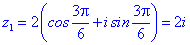
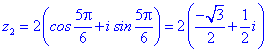
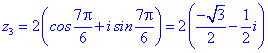
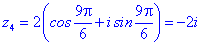
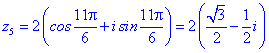
Їх аргументи перевіряємо з допомогою математичного пакету Maple. Графік шестикутника та округлені значення коренів можна переглянути нижче
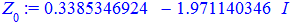
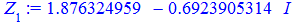
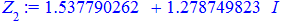
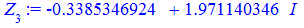
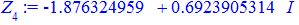
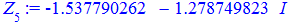
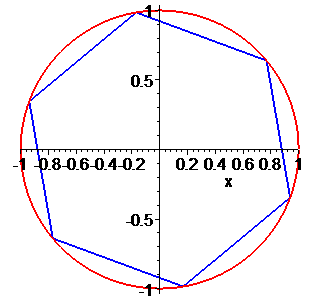
Наведений розрахунковий код для розв'язування комплексних рівнянь в Maple та побудови многокутника аргументів ви можете завантажити за посиланням нижче. З його допомогою можна знаходити корені однотипних рівнянь будь-якого порядку.
