Алгоритм обчислення інтегралу раціонального дробу
- Виділити цілу частину (якщо дріб неправильний)
- Розкласти правильний дріб на найпростіші дроби
- Проінтегрувати цілу частину та найпростіші дроби Який вигляд мають дроби при розкладі Ви можете перечитати з попереднього уроку.
Залежно від вигляду найпростіших дробів інтеграл раціонального дробу рівний одному з наведених нижче варіантів 
Тому видрукуйте або випишіть подані формули та переходьте до готових інтегралів.
Хто глибше хоче почитати теорію і розібратися в деталях, можете переглянути наступний матеріал
Приклад 1. В дробових функціях такого виду в чисельнику додають та віднімають сталу (3), яка міститься в знаменнику. В такий спосіб можна розділити чисельник на знаменник націло та отримати найпростіший дріб, інтеграл якого рівний логарифму натуральному від модуль функції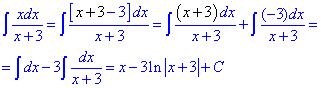
Далі так детально розписувати не будемо, але Ви про це маєте пам'ятати.
Приклад 2. Знайти інтеграл 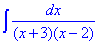
Бачимо, що маємо неправильний дріб, який розбиваємо на два прості.
Методом невизначених коефіцієнтів знаходимо множники при дробах. 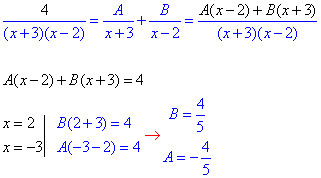
Зауважте, що тут підставляли нулі знаменника. Такий метод спрощує обчислення, оскільки при класичному підході слід виписати вирази при змінній в 0-му та 1-му степені та розв'язати систему лінійних алгебраїчних рівнянь {-2A+3B=4, A+B=0}.
Результати в обидвох варіантах отримаєте ті самі, а от шлях і час обчислень різний.
Що Вам легше виконувати вибирайте самостійно, спершу розв'язавши з десяток інтегралів першим та другим методом.
Ми ж підставляємо отриманий розклад в інтеграл та через табличні інтеграли записуємо 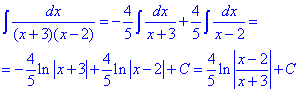
Вкінці за властивістю логарифма записали результат компактніше.
Приклад 3. Непростий, на перший погляд, інтеграл зводиться до I типу елементарних дробів заміною змінних.
Тут можна було вираз 1/(t2-2) розкласти на прості дроби, які фігурують в чисельнику та знаменнику логарифма.
Але ми цього не робили, оскільки часто наведеним представленням логарифма частки користуємося для кінцевого запису подібних інтегралів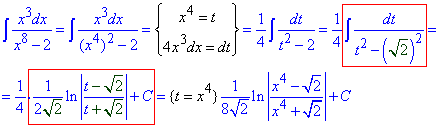
Ви також можете цей перехід виписати та користуватися при інтегруванні.
Приклад 4. В знаменнику маємо (1+x2)2, тому багато хто з Вас захоче розписати через прості дроби. Так можна робити, але це довгий шлях.
Простіший спосіб полягає у тому, щоб змінну внести під диференціал, та зробивши заміну змінних (t=x2), швидко звести інтеграл до табличного 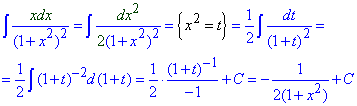
Приклад 5. Перший спосіб полягає в тому, щоб в знаменнику виділити повний квадрат.
В результаті інтегрування отримаємо логарифм частки лінійних функцій 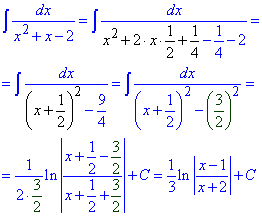
Другий спосіб полягає в знаходженні нулів знаменника та розкладі дробової функції з квадратним тричленом в знаменнику через прості дроби.
Для цього застосовуйте метод неозначених коефіцієнтів A/(x-1)+B/(x+2), отримаєте значення A=1/3, B=-1/3.
А далі при інтегруванні за II формулою отримаємо логарифми
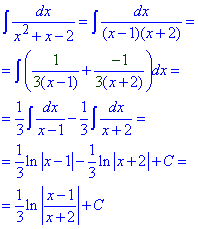
Приклад 6. Раціональний дріб 1/(x2+x-2) розкладаємо на простіші методом неозначених коефіцієнтів, прийдемо до того, що
1/(x2+x-2)=1/(x2+1)-1/(x2+2).
Останні дробові функції при інтегруванні дадуть арктангенси
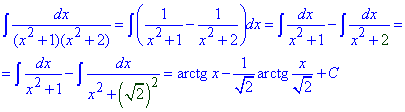
(Ще 2 приклади зі збірника задач Б. П. Демидович)
Приклад 7 (1736). Методом неозначених коефіцієнтів розкладаємо дробову функцію на прості дроби, перший з яких зводимо під логарифм частки одночленів, другий – арктангенс. Усі переходи перегляньте та запам'ятайте з наведених нижче формул 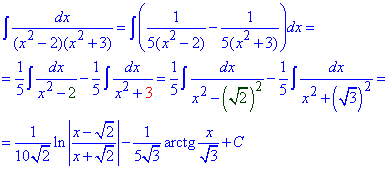
Приклад 8 (1737). Тут в штучний спосіб додали та відняли двійку в знаменнику, щоб отримати один з множників знаменника. Не буде помилкою, якщо додасте та віднімете 3, тоді спростите з другим множником. А все, що залишиться після розкладу методом неозначених коефіцієнтів розбиваєте на прості дроби I типу. При інтегруванні отримаємо логарифми, які за властивостями логарифм-функції записуємо компактно.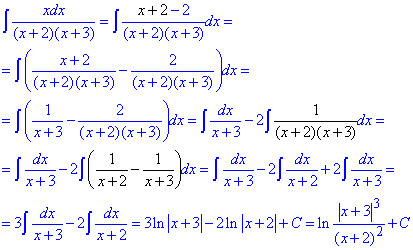
Тут вираз під логарифмом у знаменнику не брали за модулем, оскільки він в парному степені, отже додатний.
І таких прикладів у Вас буде чимало, чим більше проінтегруєте самостійно, тим краще будете розуміти всі тонкощі теми.


