Розберемо відповіді до завдань на обчислення поверхневих інтегралів другого роду по поверхні сфери та еліпсоїда. Загалом методика годиться для будь-яких поверхонь, але через великі формули тут розберемо два приклади. Ви навчитеся переходити від інтегралів другого роду до першого роду через напрямні косинуси, шукати їх, розставляти межі в подвійному інтегралі.
Завдання 1 Обчислити поверхневий інтеграл другого роду
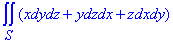
де S- зовнішня сторона сфери x2+y2+z2=a2.
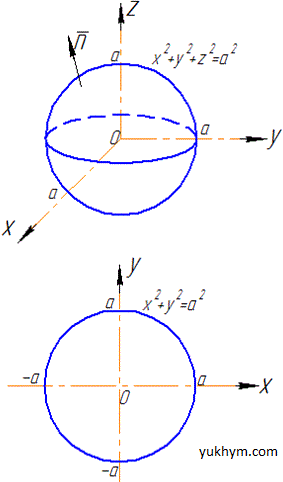
Розв'язання: Оскільки сфера складається з двох півсфер (верхньої і нижньої половини), то для зменшення обчислень поверхневий інтеграл обчислюють по верхній половині сфери (для z≥0), а результат подвоюють:
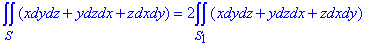
Це стосується всіх поверхонь симетричних відносно площини z=0.
Поверхневий інтеграл 2-го роду зведемо до поверхневого інтеграла 1-го роду наступним через елементи площі ds та напрямні косинуси:
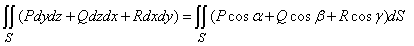(1)
де P=P(x, y, z)=x, Q=Q(x, y, z)=y , R=R(x, y, z)=z.
Теорію тут давати не будемо, лише практика.
З канонічного рівняння сфери x2+y2+z2=a2 виразимо координату z як функцію z(x,y)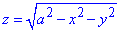
(перед коренем беремо знак «+», оскільки розглядаємо верхню півсферу).
Далі знайдемо часткові похідні першого порядку z(x,y) за змінними x,y:
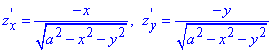- часткові похідні першого порядку.
З часткових похідних знаходимо множник
(*)
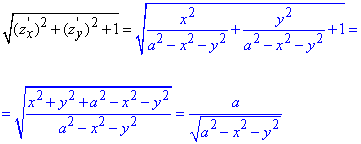який пов'язує елемент поверхні з елементом площі (dx, dy)
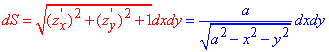
Напрямні косинуси поверхні теж містять множник (*) в знаменнику та часткові похідні в чисельнику.
Формула для обчислення напрямних косинусів має вигляд:
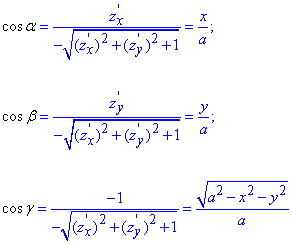
Перед радикалами (коренями) взятий знак «-», оскільки нормаль поверхні верхньої півсфери утворює гострий кут з віссю Oz, тобто cos(hamma)>0.
Обчислимо заданий поверхневий інтеграл 2-го роду:
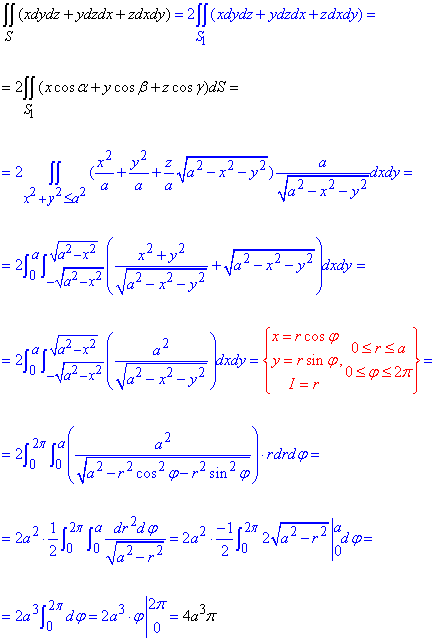
В ході інтегрування перейшли до полярної системи координат, перерахували межі інтегрування. Оскільки маємо подвійний інтеграл, то слід підінтегральний вираз помножити на якобіан переходу I=r.
Більше пояснень дає сама формула, яку Вам слід проаналізувати до дрібниць.
Розв'яжемо ще один приклад на подібну поверхню інтегрування.
Завдання 2 Обчислити поверхневий інтеграл другого роду
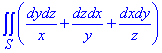
де S- зовнішня сторона еліпсоїда x2/a2+y2/b2+z2/c2=1.
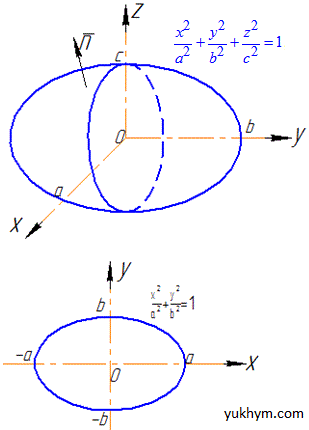
Розв'язання: Еліпсоїд як і сфера містить симетричні частини (верхньої і нижньої половини), то поверхневий інтеграл шукаємо по верхній половині еліпсоїда (для z≥0), а результат множимо на двійку:
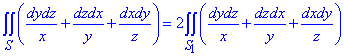
Повторимо формулу переходу від поверхневий інтегралу ІІ роду до інтегралу І роду :
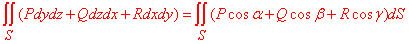
тут P=P(x, y, z)=1/x, Q=Q(x, y, z)=1/y , R=R(x, y, z)=1/z.
З рівняння поверхні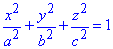 
виражаємо "зет" через дві інші координати
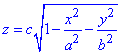
Корінь беремо з додатним знаком, оскільки нас цікавить верхня частина.
Далі обчислюємо
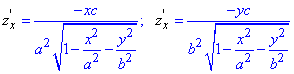
- часткові похідні першого порядку.
Підставляємо та знаходимо множник для диференціала поверхні
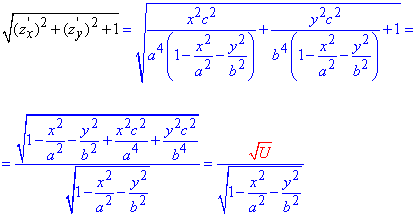
звідси
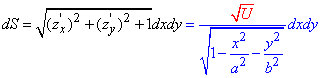
тут позначили для спрощення формул
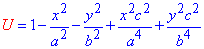
За відомою формулою обчислюємо напрямні косинуси до поверхні еліпсоїда:
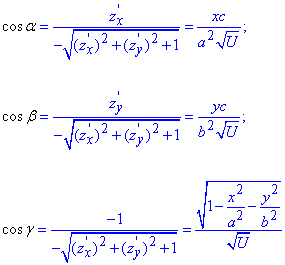
Перед коренем взятий знак «-», так як нормаль поверхні півеліпсоїда утворює гострий кут з віссю Oz.
Обчислимо поверхневий інтеграл 2-го роду:
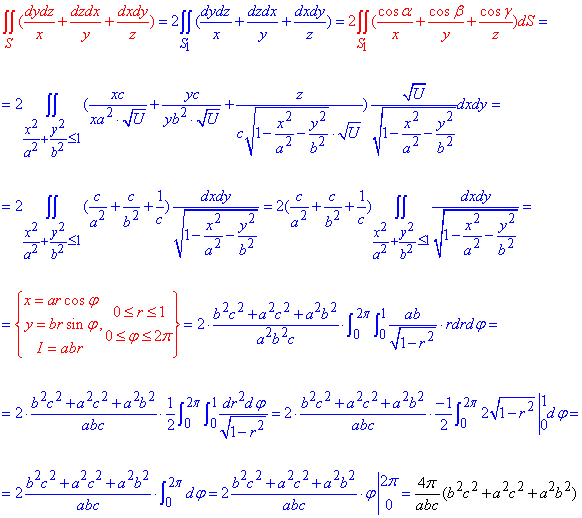
По аналогії з попереднім прикладом під інтегралом переходимо до полярних координат, враховуємо якобіан, а далі вже з перерахованими межами обчислюємо інтеграл. Щоб обчислити внутрішній інтеграл "r" внесли під диференціал, щоб утворити ідентичний диференціал, як функція в знаменнику під коренем d(1-r2).
Зовнішній інтеграл від сталої дає значення кута, підставляємо межі і дістаємо красиву формулу.
Знаємо, що Вам не просто даються поверхневі та кратні інтеграли, тому постійно наповнюємо новими прикладами, охоплюємо більше практичних завдань та пояснюємо всі можливі методики інтегрування, які можуть у Вас вимагати викладачі.
Також виконуємо розрахункові та контрольні на замовлення.
Залишайтеся з нами та отримуйте лише задоволення від навчання!
