Формула Стокса дає можливість перейти від інтеграла по поверхні до інтеграла по границі поверхні, і навпаки. Важливо щоб обхід контуру узгоджувався з вибраною стороною поверхні (всередину або назовні).
Наведемо формулу Стокса
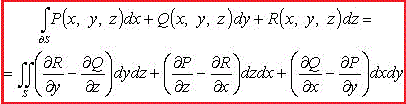
Далі в прикладах будемо використовувати компактний запис формули через визначник. Загалом поверхневі та криволінійні інтеграли досить важко обчислювати, на це йде багато часу як на практичних так і при самостійних розрахунках.
Завдання 1 Використовуючи формулу Стокса, обчислити інтеграл
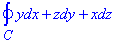
де С- коло x2+y2+z2=a2, x+y+z=0, що пробігається проти ходу годинникової стрілки, якщо дивитись з додатної сторони осі Ox.
Розв'язання: Криволінійний інтеграл 2-го роду зведемо до поверхневого інтеграла першого роду, використовуючи формулу Стокса:
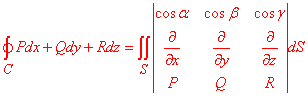
тут потрібно підставити свої функції, які беремо з підінтегральної
P=P(x, y, z)=y, P=P(x, y, z)=z, P=P(x, y, z)=x.
Пройдемося по алгоритму обчислення інтегралу, щоб Ви бачили, що за чим потрібно робити.
Спершу потрібно знайти диференціал ds і напрямні косинуси поверхні, яку обмежує крива:
з рівняння сфери x2+y2+z2=a2 виражаємо z(x,y)
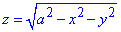(перед коренем знак «+»).
Обчислюємо часткові похідні
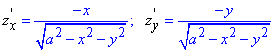
та підставляємо в формулу диференціала поверхні
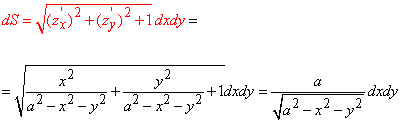
Знайдемо напрямні косинуси заданої поверхні:
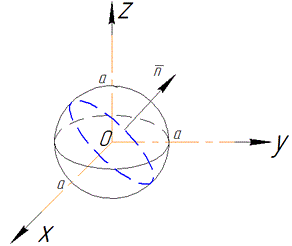
Оскільки сфера x2+y2+z2=a2 перетинається площиною x+y+z=0, то нормальний вектор площини:
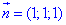
тоді норма вектора
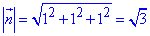
Можемо записати напрямні косинуси
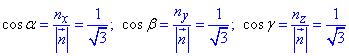
Обчислимо заданий криволінійний інтеграл 2-го роду за формулою Стокса:
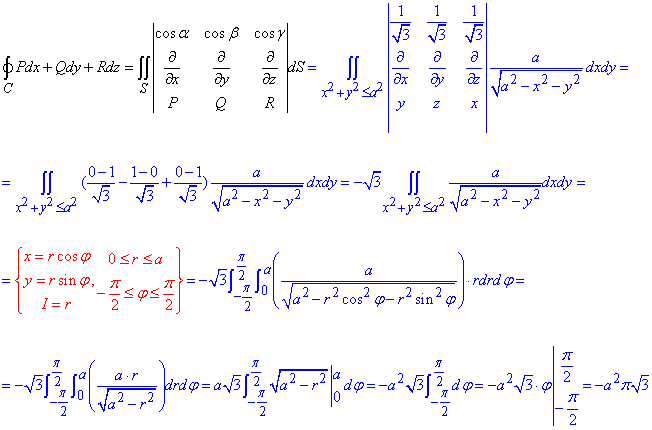
При інтегруванні перейшли до полярної СК. Оскільки маємо кратний інтеграл, то помножили на якобіан переходу, далі розставили межі та проінтегрували.
Формула інтегрування, можливо, незручна для перегляду на мобільних, але багато з Вас зможуть розібратися з інтегралом.
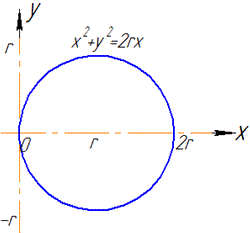
Завдання 2 Використовуючи формулу Стокса, обчислити інтеграл
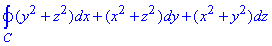
де C- крива x2+y2+z2=2Rx, x2+y2=2rx (0<r<R, z>0), яка пробігається так, що обмежена нею найменша область на зовнішній стороні сфери залишається зліва.
Розв'язання: Повторно наведемо формулу зведення криволінійний інтеграла другого роду до поверхневого інтеграла першого роду через формулу Стокса:
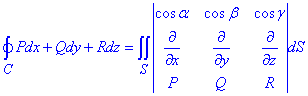
Випишемо підінтегральні функції
P=P(x, y, z)=y2+z2, Q=Q(x, y, z)=x2+z2 , R=R(x, y, z)=x2+y2.
Виконуємо розрахунки для знаходження диференціалу dS та напрямних косинусів поверхні:
з рівняння x2+y2+z2=2Rx отримаємо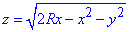 
Беремо часткові похідні першого порядку по "ікс, ігрик"
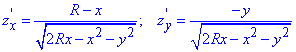
Обчислюємо диференціал
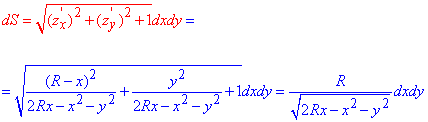
Знайдемо напрямні косинуси поверхні за формулами:
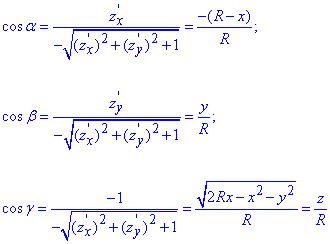
Перед радикалами беремо знак «-», оскільки нормаль поверхні утворює гострий кут з віссю Oz.
Наперед обчислимо визначник, що стоїть під знаком поверхневого інтеграла:
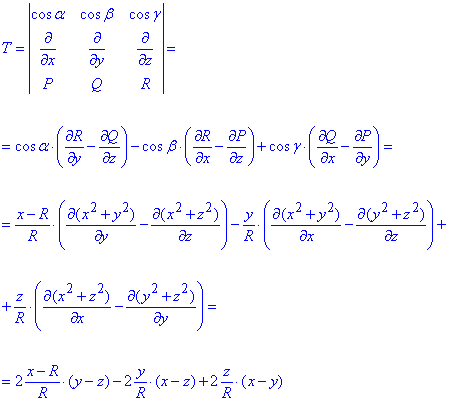
Криволінійний інтеграл 2 роду обчислюємо за формулою Стокса:
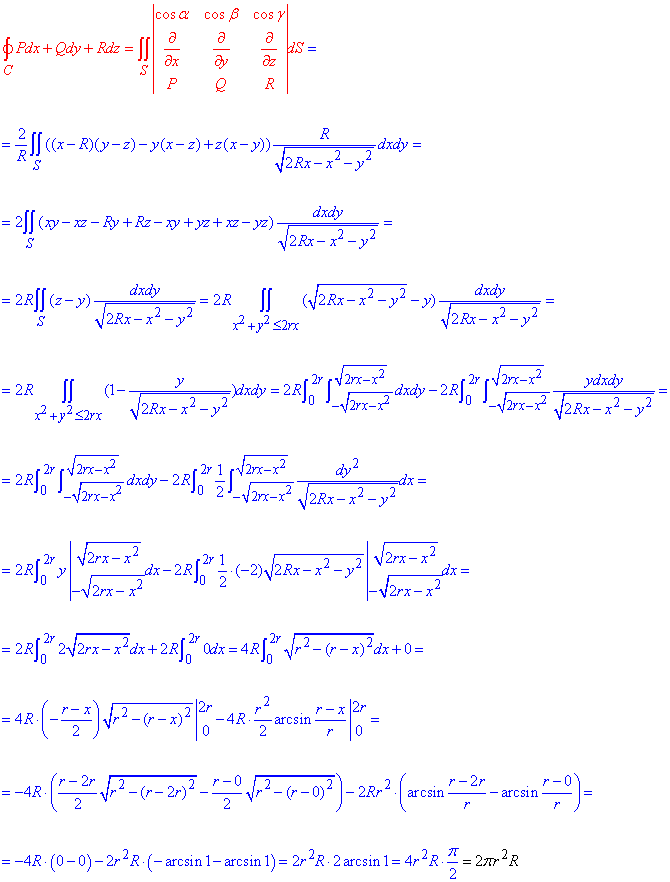
Кінцеве значення компактне, проте щоб його отримати довелось використати не один листок А4 . Якщо є бажання можете роздрукувати формулу та детальніше проаналізувати подвійний інтеграл.
Завдання 3 Використовуючи формулу Стокса, обчислити інтеграл
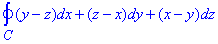
де C- еліпс x2+y2=a2, x/a+z/h=1 (a>0,h>0), що пробігається проти ходу годинникової стрілки, якщо дивитись з додатної сторони осі Ox.
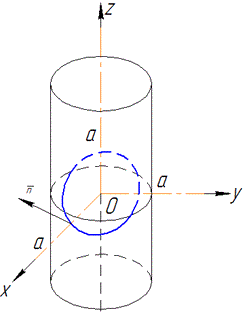
Розв'язання: Інтеграл 2-го роду зводимо до поверхневого інтегралу 1 роду за формулою Стокса:
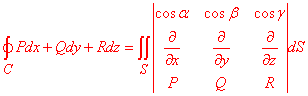
Виписуємо функції P=P(x,y,z)=y-z, P=P(x,y,z)=z-x, P=P(x,yxz)=x-y.
Перетворюємо друге рівняння x/a+z/h=1 щоб виразити "зет"
.
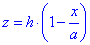Тоді похідна рівна
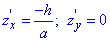
Бачимо, що отримали функцію незалежну від координати "ігрик", тому похідна по ній рівна нулю.
Пам'ятайте про це коли прийде час шукати диференціал поверхні
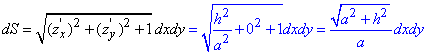
Поміркуємо як знайти напрямні косинуси до поверхні:
Оскільки циліндр x2+y2=a2 перетнутий площиною x/a+z/h=1, то нормальний вектор площини:
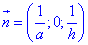
Подумайте, чому саме так!
Обчислюємо модуль нормалі
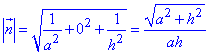
та необхідні для інтегрування косинуси
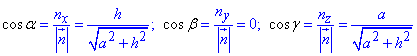
За формулою Стокса знаходимо криволінійний інтеграл другого роду :
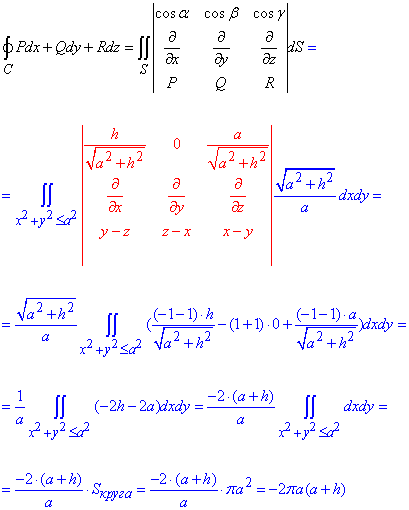
Наприкінці розрахунків використали формулу площі круга з радіусом R=a
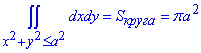
Якщо зможете повторити самостійно на подібному прикладі, і правильно знайдете інтеграл, то Ви на хорошому рівні вивчили інтегрування!
