Подвійний інтеграл. Межі інтегрування

Подвійні інтеграли використовують в математиці, механіці, фізиці. З його допомогою можна вирішити безліч непростих задач. Нижче наведено 10 прикладів на подвійні та потрійні інтеграли, які в значній мірі полегшать підготовку до контрольної роботи чи екзамену. Приклади взяті з індивідуальної роботи з вищої математики, заданої студентам ЛНУ ім. І. Франка.

ВАРІАНТ – 12

Подвійний інтеграл

ЗАВДАННЯ 1.18 Змінити порядок інтегрування в подвійному інтегралі:

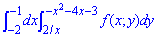
Розв'язання: Спершу записуємо область інтегрування, що обмежена границями

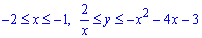
де y=2/x - гіпербола.
y=-x²-4x-3 - парабола з вершиною у точці S(-2;1), гілками вниз.
Щоб знати, як розставити межі інтегрування при зміні меж інтегрування зобразимо область інтегрування на площині
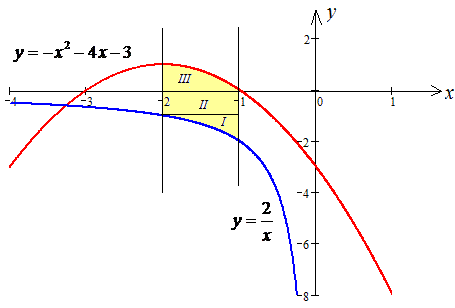Виразимо отримані функції через змінну y:
y=2/x, звідси x=2/y; y=-x²-4x-3, звідси 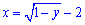, перед радикалом стоїть знак «+» оскільки частина параболи знаходиться у правій (додатній по x=-2) частині півплощини.
З рисунку бачимо, що при зміні порядку інтегрування область необхідно розділити на три: D=D₁+D₂+D₃.
Розставимо межі в кожній області:

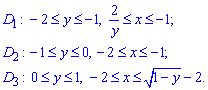
Змінюємо порядок інтегрування функції
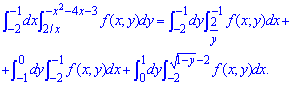Як бачите нічого важкого немає, головне уявляти графік функції та мати точки їх перетину - межі інтегрування.

ЗАВДАННЯ 2.19 Знайти площу плоскої фігури, заданої наступними умовами: y=2^x,y=5,2x-2y+3=0.
Розв'язання: Перш за все виконуємо побудову усіх кривих, щоб бачити як змінюються межі інтегрування
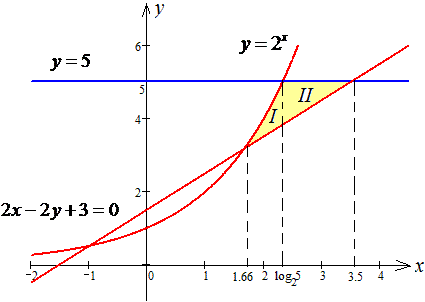Далі знайдемо точки перетину графіків заданих функцій: 1 та 2

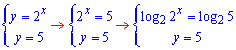
звідси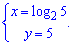
Дал точки перетину 2 та 3 функцій

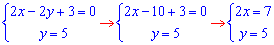
звідси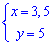
Наостанок перетин 1 та 3 ф-й

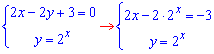
звідси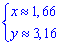
Отож, задану область будемо розбивати на дві області: D=D₁+D₂.
Розставимо межі для кожної з областей:

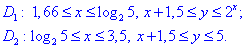
Через подвійний інтеграл знаходимо площу фігури, обмеженої заданими кривими:
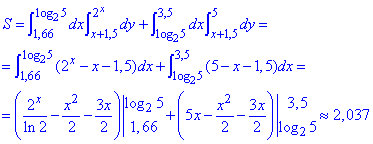Функції не важкі для інтегрування, тому в передостанньому виразі підставте межі самостійно.
При округленні площа криволінійної трапеції рівна 2,037 одиниць квадратних.

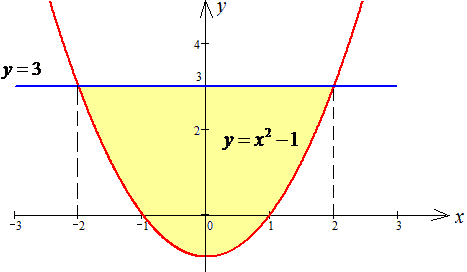
ЗАВДАННЯ 3.20 Знайти подвійний інтеграл 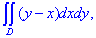по області D, обмеженій вказаними лініями: D: y=x²-1,y=3.
Розв'язання: Знайдемо точки перетину графіків заданих функцій: y=x²-1 і y=3:
3=x²-1, x²-4=0, (x-2)(x+2), x=-2; x=2.
Параболу та пряму зобразимо графічно
Розставимо межі в заданій області D:

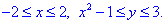
Обчислимо подвійний інтеграл по області, обмеженій парабоою і прямою:
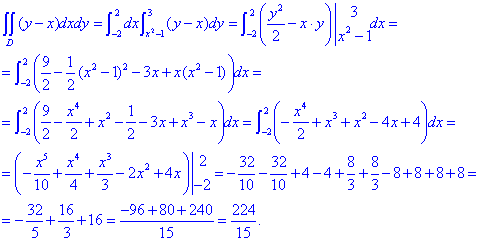Визначений інтеграл рівний I=224/15=14,9(3).

ЗАВДАННЯ 4.21 Знайти подвійний інтеграл, використовуючи полярні координати:

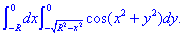
Розв'язання: Побудуємо область інтегрування, яка обмежена кривими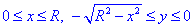
де 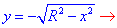y=R²-x², x²+y²=R²
Отримали коло з центром у точці O(0;0) і радіусом R (нижня половина).
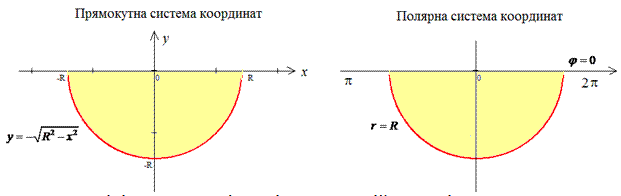Використовуючи заміну змінних

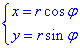
перейдемо до полярної системи координат (СК).
При цьому підінтегральну функцію слід домножити на якобіан переходу, який знаходимо через визначник похідних:

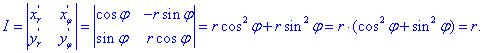
Перепишемо підінтегральну функцію в полярній СК :

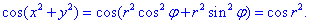
Межі інтегрування при переході до полярної системи координат зміняться на такі:

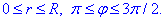
Обчислимо подвійний інтеграл:
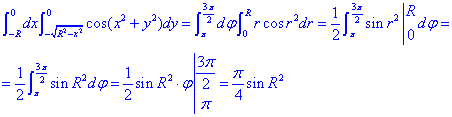Він рівий I=Pi/4*sin(R²).

.
ЗАВДАННЯ 5.22 Обчислити площу області D, обмеженої вказаними лініями: D: x³=3y, y²=3x.
Розв'язання: Знайдемо точку перетину двох графіків 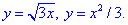: 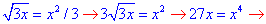x₁=0, y₁=0; x₂=3, y₂=3.
Графік кривих в декартовій системі координат має вигляд
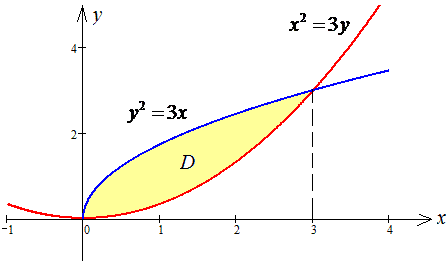Розставимо межі в заданій області D:

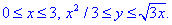
Знайдемо площу криволінійної трапеції, обмеженої вказаними лініями:
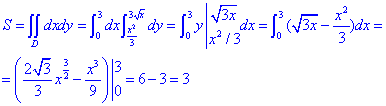Площа рівна 3 одиниці квадратні.

ЗАВДАННЯ 6.23 Використовуючи подвійний інтеграл, обчислити, перейшовши до полярних координат, площу плоскої фігури: (x²+y²)³=4a²xy(x²-y²).
Розв'язання: Спершу побудуємо чотирьох пелюстник
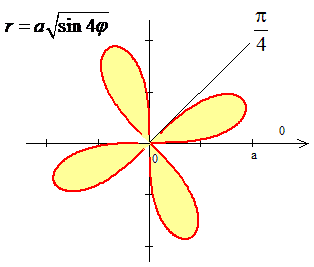Перейдемо до полярної системи координат:

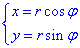
Якобіан переходу рівний I=r.
Знайдемо межі інтегрування в новій системі координат

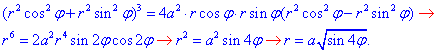
Змінні пробігають значення:

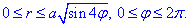
Розставляємо межі в подвійному інтегралі, таким чином знайдемо чверть площі плоскої фігури. Далі результат помножимо на 4:
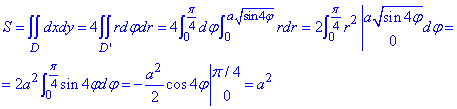Площа рівна S=a² одиниць квадратних.

ЗАВДАННЯ 7.24 Обчислити об'єм тіла, заданого поверхнями, що його обмежують: y²+z²=6z, x=8-y², x=0.
Розв'язання: Перетворимо рівняння y²+z²=6z до класичного вигляду y²+(z-3)²=3²- коловий циліндр з радіусом R=3 і витягнутий вздовж осі Ox.
Друге рівняння x=8-y² - параболічний циліндр витягнутий вздовж осі Oz.
Запишемо функції заданих поверхонь в тій площині, де шукатимемо об'єм:

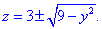
Наведемо приблизний вигляд тіла, об'єм якого шукаємо та область інтегрування (проекцію тіла в декартову площину)

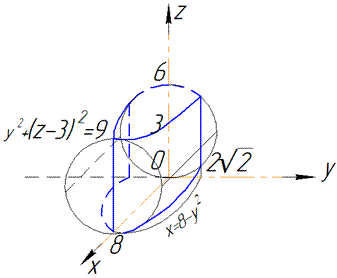
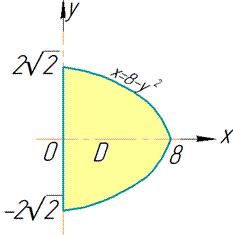
Об'єм тіла, що обмежене заданими поверхнями, знайдемо як різницю об'ємів колового циліндра y²+(z-3)²=3², що обмежений площинами x=0 і x=8, а також параболічного циліндра x=8-y², який обмежений площинами z=0 і z=6.
При розставлянні меж враховуємо парність заданих функцій відносно осі Ox , тому результат помножимо на 2.
Розставимо межі в заданій області:

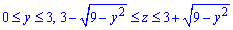
Через подвійний інтеграл знайдемо об'єм тіла, що обмежене коловим циліндром.
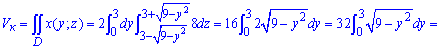переходимо під інтегралом до полярних координат
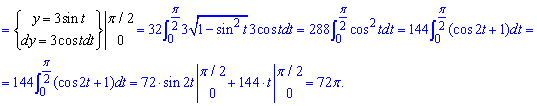Наступним знаходимо об'єм тіла, обмеженого параболічним циліндром.
Розставимо межі в заданій області

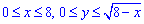
та обчислимо подвійний інтеграл
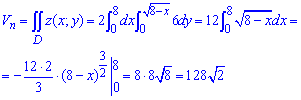Об'єм тіла, що обмежене коловим і параболічним півциліндром рівний
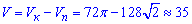35 куб. од.
Уважно проаналізуйте як визначати межі інтегрування. Це найважче, що може бути в подібних задачах.
Як обчислити визначений інтеграл, як правило, повинні знати усі студенти. Тут лише розширюється його застосування.

Потрійний інтеграл

ЗАВДАННЯ 8.25 Розставити межі інтегрування в потрійному інтегралі 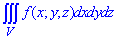, якщо область V обмежена вказаними поверхнями: V: x=2, 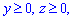y=3x, z=4(x²+y²).
Намалювати область інтегрування.
Розв'язання: Рівняння поверхні в просторі z=4(x²+y²) - еліптичний параболоїд.
Графік параболоїда та проекція в декартову площину тіла мають вигляд
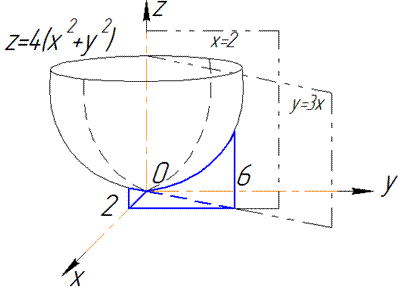
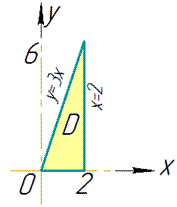Межі інтегрування розставимо наступним чином:
V: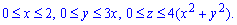
Розставляємо межі інтегрування відповідно до області

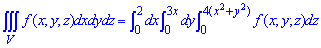
ЗАВДАННЯ 9.6 Обчислити потрійні інтеграли:

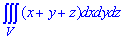
де V: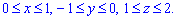
Розв'язання: Виконаємо побудову області інтегрування
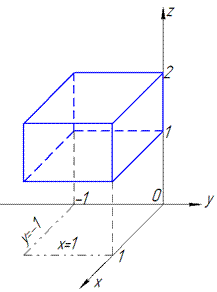Задана область V є паралелепіпедом, тому без труднощів розставляємо межі інтегрування та від внутрішнього до зовнішнього знаходимо інтеграл

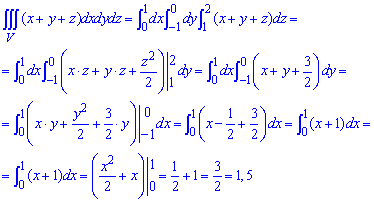
Обчислення не складні, тому перетворення в формулі проаналізуйте самотійно.

ЗАВДАННЯ 10.7 Використовуючи потрійний інтеграл, обчислити об'єм тіла: де z=x², x-2y+2=0, x+y=7, 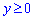. Намалювати область інтегрування.
Розв'язання: Забігаючи вперед, зобразимо тіло та його проекцію
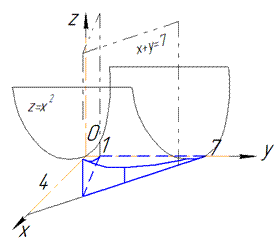
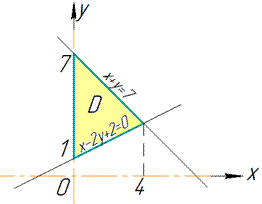Це допоможе визначити межі інтегрування

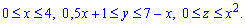
За допомогою потрійного інтегралу обчислюємо об'єм тіла, обмеженого поверхнями:

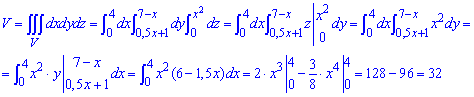
Визначені інтеграли не важкі, після їх знаходжень маємо об'єм 32 одиниці кубічні.

На цьому індивідуаьна робота з вищої математики вирішена. Більше прикладів на застосування інтегралу шукайте на сторінах сайту. Якщо важко вирішити контрольну роботу чи індивідуальні завдання, тоді звертайтеся за допомогою!