Обчислення подвійних та потрійних інтегралів

Правильно розставити межі в подвійному та потрійному інтегралах не таке важке і завдання, особливо якщо виконана побудова області інтегрування чи маєте уявлення просторового тіла. Та в більшості випадків - на практиці, контрольній чи екзамені студенти не мають можливості якісно виконати графічний аналіз, візуально проаналізувати області, а ще більша проблема, що багато з них не володіють технікою зміни порядку інтегрування. В окремих задачах такий підхідхід дозволяє звести обчислення від інтегрування по 2 -3 областях до однієї. В результаті швидо вдається знайти площу криволінійної трапеції (фігури на площині) чи об'єму тіла. Для кругових, еліптичних та різних пелюсткових фігур доцільно виконувати перехід до полярних координат, а вже в них через кілька визначених інтегралів знайти площу чи об'єм. Детальний розбір готових відповідей до вказаних задач дозволяє в швидкий термін вивчити методику та краще розуміти теоретичний матеріал на кратні інтеграли. Усі завдання взяті з індивідуальної роботи для студентів ЛНУ ім. І. Франка, варіанти добре підібрані та охоплюють кілька тем з вищої математики.

ВАРІАНТ – 5

Обчислення подвійних інтегралів

ЗАВДАННЯ 1.23 Поміняти порядок інтегрування в подвійному інтегралі:
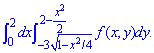Розв'язання: Методика обчислень до таких задач полягає в наступному:
спершу виписуємо область інтегрування з інтегралу, яка обмежена кривими

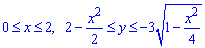
Далі перетворюємо функції, щоб знайти їх канонічний вигляд.
Верхня межа y=2-x²/2 - парабола з вершиною в точці O(0;2) і вітками вниз.
Зводимо до канонічного вигляду нижню межу інтегрування

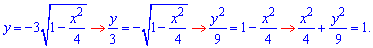
Отримали півеліпс з центром у точці S(0;0) і півосями a=2, b=3.
Зобразимо криві в декартовій системі координат (СК)
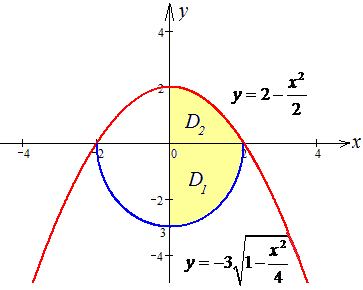Виразимо отримані функції через змінну y:
З першої 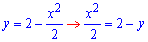отримаємо кореневу залежість 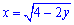, перед радикалом стоїть знак «+» оскільки частина параболи знаходиться у правій (додатній по x) частині півплощини;
Для еліпса матимемо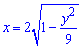
При зміні порядку інтегрування область потрібно розбити на дві частини: D=D₁+D₂.
Розставимо межі в кожній половині:

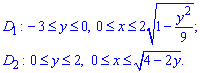
Змінюємо межі в подвійному інтегралі

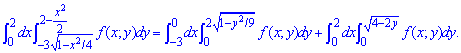
ЗАВДАННЯ 2.24 Знайти площу плоскої фігури, заданої наступними умовами: y=x²-4x+3, y=x+1,y=-2x+5.
Розв'язання: Завдання досить творче, адже шукана фігура має наступний графік. Але це забігаючи наперед
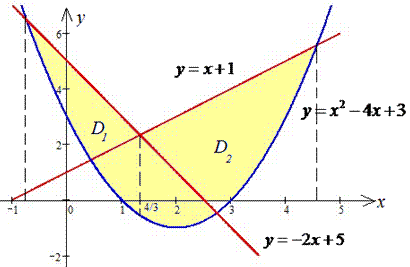На практиці Ви цього не знаєт, тому починаєте аналіз з пошуку точок перетину графіків заданих функцій: Спершу 1 та 2

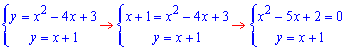
звідси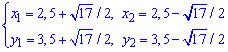
Далі 2 і 3

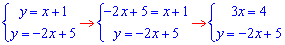
звідси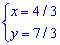
І наостанок 1 і 3

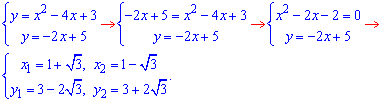
Координати точок перетину містять корені, що означає що викладач, що готував завдання особливо не заморочувався, щоб полегшити роботу студентам та отримати вкінці хорошу відповідь.
Задану область можна розбивати на 2-4 частини, все залежить від порядку інтегрування.
Ми ж задану область будемо розбивати на дві області: D=D₁+D₂, як на малюнку.
Розставимо межі в кожній області:

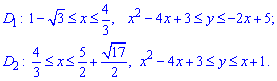
За допомогою подвійного інтегралу обчислимо площу фігури, обмеженої параболою і лініями:

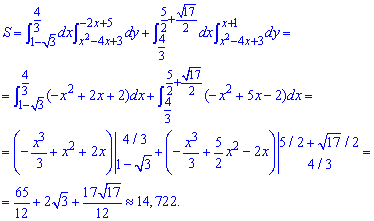
Інтегрувати не важко, однак коментувати межі вдруге не будемо.

ЗАВДАННЯ 3.25 Обчислити подвійний інтеграл по області D, обмеженій вказаними лініями:
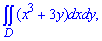, D: x+y=1, y=x²-1, .

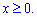Розв'язання: Знайдемо точки перетину графіків заданих функцій: y=1-x і y=x²-1:
1-x=x²-1, x²+x-2=0, (x-1)(x+2)=0,x=1,y=0.
Зобразимо область інтегрування в декартовій СК
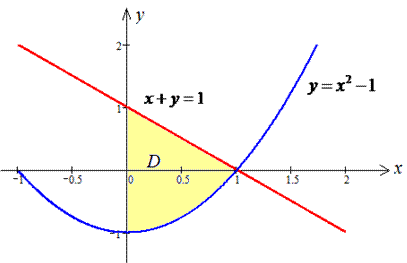Розставимо межі від параболи до прямої, і по зміні аргументу:

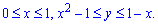
Обчислимо подвійний інтеграл заданої функції: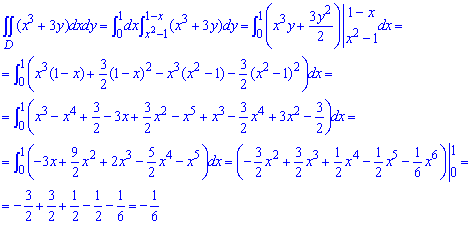
.
Отримали від'ємний інтеграл I=-1/6.

ЗАВДАННЯ 4.6 Обчислити подвійний інтеграл, використовуючи полярні координати: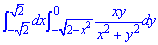

Розв'язання: Зведемо функції меж інтегрування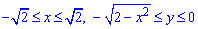 до канонічного вигляду

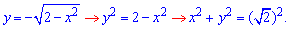
Отримали коло з центром у точці O(0;0) і радіусом корінь з двох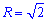 (нижня половина).
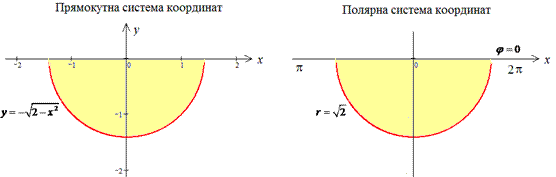Для переходу до полярної системи координат застосовуємо заміну змінних:

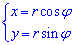
При цьому підінтеграьну функцію слід помножити на якобіан переходу:
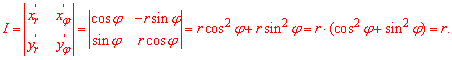Перетворимо підінтегральну функцію під полярні координати:

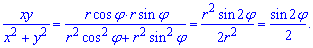
Запишемо межі інтегрування в полярній системі координат:

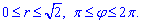
Обчислимо подвійний інтеграл в полярній СК:
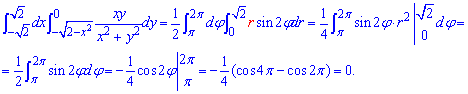Він рівний 0, що означає, що підінтегральна функція непарна в заданій області. Це легко бачити з її початкового запису.

ЗАВДАННЯ 5.7 Обчислити площу області D, обмеженої вказаними лініями: D: y²=4x, x²=4y.

Розв'язання: За інструкцією знаходимо точку перетину двох графіків
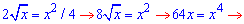x₁=0, y₁=0; x₂=4; y₂=4.
Розставимо межі в заданій області D:

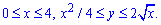
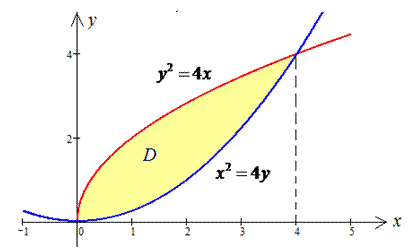
Побудуємо графік фігури за відомими рівняння ф-й
Площу фігури знаходимо за формулою:
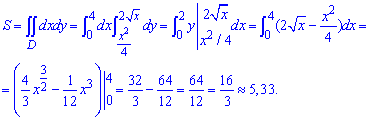Внутрішній інтеграл передбачає підстановку меж інтегрування і лише в зовнішньому доводиться затосувати формули інтегрування. Площа фігури рівна S=16/3 одиниць квадратних.

ЗАВДАННЯ 6.8 Використовуючи подвійний інтеграл, обчислити, перейшовши до полярних координат, площу плоскої фігури: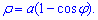

Розв'язання: Рівняння rho=a(1-cos(phi)) описує кардіоїду в полярній системі координат.
Графік кардіоїди має вигляд
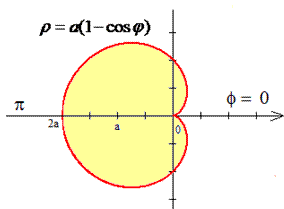Оскільки задана функція парна, то обчислимо половину площі і результат помножимо на 2.
Записуємо межі інтегрування для верхньої половини фігури:

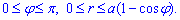
Через подвійний інтеграл знаходимо площу кардіоїди:
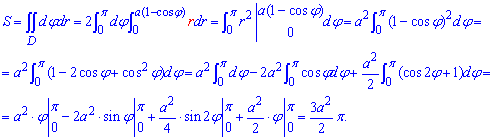Під інтегралом довелося застосувати формули пониження степеня для квадрату косинуса. Також, зверніть увагу, що в усіх прикладах при знаходженні інтегралів в полярних координатах функція під інтегралом має містити множником якобіан переходу r.

Обчислення потрійних інтегралів

ЗАВДАННЯ 7.9 Знайти об'єм тіла, заданого поверхнями, що його обмежують: x²/9+y²/4+z²=1, x²+y²=2x, z=0,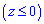

Розв'язання: Перша поверхня x²/9+y²/4+z²=1 - еліпсоїд з півосями a=3, b=2, c=1.
Другу зведемо до канонічного вигляду x²+y²=2x, (x-1)²+y²=1² - коловий циліндр витягнутий вздовж осі Oz.
Запишемо функції заданих поверхонь в тій площині, де шукатимемо об'єм тіла:

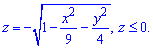
Побудуємо тримірну модель тіла і його проекцію в декартову площину

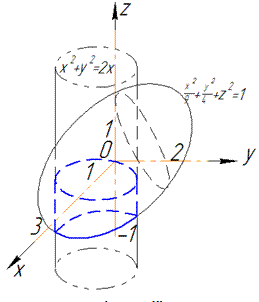
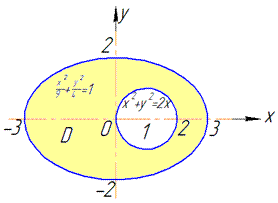
Об'єм тіла, що обмежене заданими поверхнями, знайдемо як різницю об'ємів півеліпсоїда і півцилідндра, який обмежений знизу півплощиною z=-1. При розставлянні меж будемо враховувати парність заданих функцій і результат помножимо на 2.
Спершу знайдемо об'єм тіла, що обмежене півеліпсоїдом.
Розставимо межі інтегрування в заданій області:

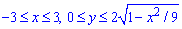
та через подвійний інтеграл знайдемо об'єм півеліпсоїда
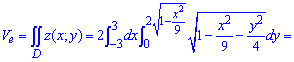згідно рекомендацій, для спрощення обчислень перейдемо до полярної системи координат (запишемо формули переходу та якобіан)
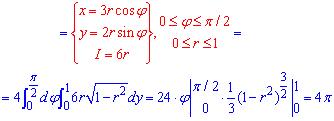Знайдемо об'єм півциліндра, що обмежений площиною z=-1.
Поверхня обмежена наступними межами:

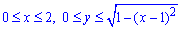
Підставляємо їх в формулу об'єму тіла і розраховуємо
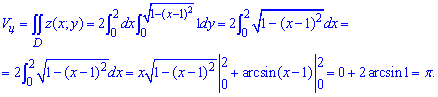Кінцевий об'єм обчислюємо як різницю між півеліпсоїдом і півциліндром:

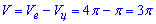
він рівний V=3Pi кубічних одиниць.

ЗАВДАННЯ 8.10 Розставити межі інтегрування в потрійному інтегралі 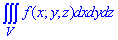, якщо область V обмежена вказаними поверхнями: V: x=2, y=4x,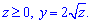
Намалювати область інтегрування.
Розв'язання: Рівняння поверхні в просторі запишемо з останньої умови: z=y²/4 - це параболічний циліндр.
Перетин поверхонь в просторі та проекція тіла в декартову площину зображено на рисунку нижче
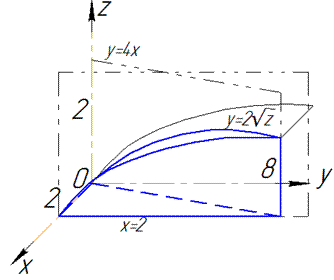
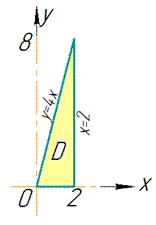Межі інтегрування розставимо наступним чином:
V: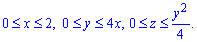
Записуємо потрійний інтеграл з врахуванням знайдених меж

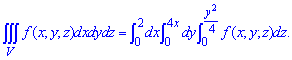
ЗАВДАННЯ 9.11 Обчислити потрійні інтеграли: 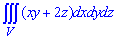, де V: , , .

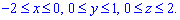Розв'язання: Виконуємо побудову поверхонь інтегрування

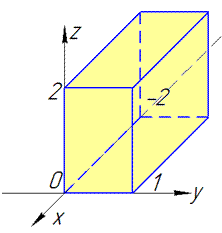
Задана область V є паралелепіпедом, крім цього підінтегральна функція задана в явному вигляді xy+2z.
Підставляємо межі в потрійний інтеграл і знаходимо його значення

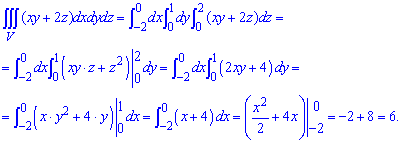
Формули інтегрування для прикладу не важкі і його під силу знайти усім.

ЗАВДАННЯ 10.12 Використовуючи потрійний інтеграл, обчислити об'єм тіла: де y=2x,y=3, 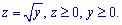Намалювати область інтегрування.

Розв'язання: Спершу виконуємо побудову допоміжного малюнка. Проекція тіла на площину дає прямокутний трикутник

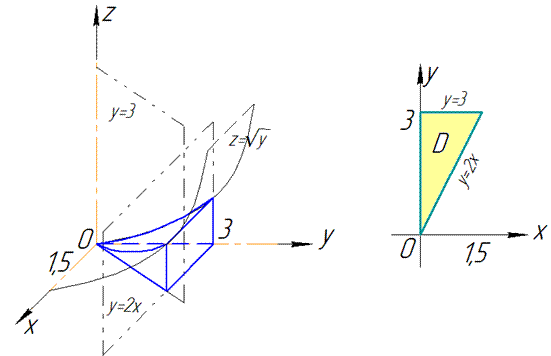
Запишемо межі інтегрування, враховуючи умову і виконаний рисунок:

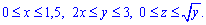
Підставимо межі в потрійний інтеграл та знайдемо об'єм тіла:

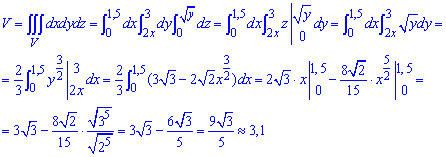
Саме інтегрування розписане в деталях, тому проаналізуйте розрахунки з формули.
На цьому контрольна з вищої математики розв'язана, висновки щодо ефективності тих чи інших прийомів кожен повинен зробити самостійно. В доповнення можемо лише сказати, що Ви завжди можете звернутися до нас за консультацією щодо обчислень подвійних та потрійних інтегралів.