Знаходження поверхневих інтегралів зводиться до застосування криволінійного інтегралу І роду, який в свою чергу приводить до обчислення повторного інтегралу. Як це реалізувати на практиці Ви зрозумієте після перегляду наступних відповідей, які підготовлені за матеріалами для студентів ЛНУ ім. І. Франка.
ЗАВДАННЯ 5.1 Обчислити поверхневий інтеграл int(1/(1+x+z)2,ds) по поверхні сігма , де 
– частина площини, що знаходиться в першому октанті :x+y+z=1
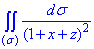
Розв'язання: Наведемо в першому ж завданні детальну інструкцію, як розв'язувати цей і всі наступні за ним приклади. На практиці все ідентично - вам будуть задані подібні умови, в більшості випадків площина лежатиме в першому октанті, підінтегральна функія не надто важка для приведення поверхневого інтегралу до невластивого, а далі до визначеного.
Спершу слід побудувати площину сігма: x+y+z=1 - бачимо що вона належить першому октанту.
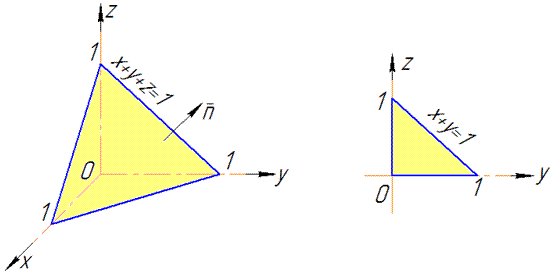
Задана площина проектується на область D в Oxy наступним чином xє[0;1], yє[0; 1-x] - це прямокутний трикутник, катети якого лежать на координатних осях.
Щоб знайти поверхневий інтеграл І роду по площині виразимо одну змінну через інші, як правило це змінна "z"
z=1-x-y та визначаємо часткові похідні
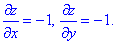
далі обчислюємо диференціал по поверхні
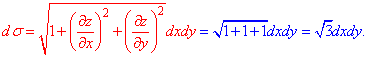
Тут зразу наведена формула диференціалу, яка відома з теорії, проте її тут часто будемо повторювати, щоб Ви могли її добре запам'ятати.
Далі поверхневий інтеграл перетворюємо до невластивого, а той в свою чергу до повторного інтегралу.
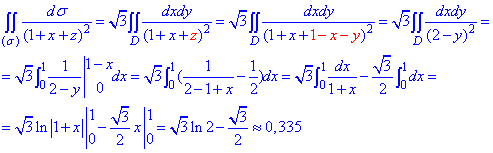
Інтегрувати задану функцію не важко, гляньте, що наперед слід визначити з рівняння поверхні змінну z - через функцію від x,y та перетворити підінтегральний вираз.
ЗАВДАННЯ 5.3 Обчислити поверхневий інтеграл int(7x+9y,ds) по поверхні сігма, де – частина площини x+y/3+z=1, що знаходиться в першому октанті
Розв'язання: Побудуємо задану площину сігма: x+y/3+z=1 в декартовій площині.
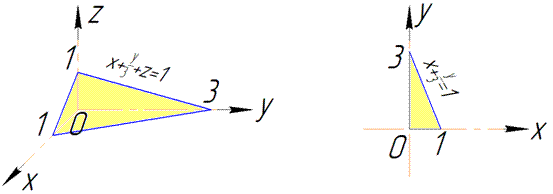
Багато хто каже, що це не вся площина, але нас цікавить перший октант, тобто та її частина де всі координати x,y,z приймають додатні значення.
Бачимо, що задана площина проектується на область D в Oxy наступним чином
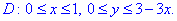
Потрібно знайти поверхневий інтеграл І роду.
Для цього виражаємо функцію z=1-x-y/3, та шукаємо частинні похідні
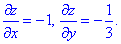
На їх основі перетворюємо формулу диференціала площі
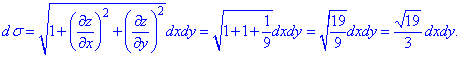
Останнім кроком переходимо від поверхневого інтегралу 1 роду до повторного та обчислюємо значення
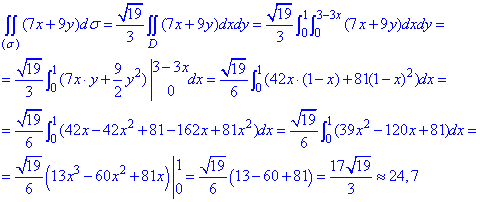
Формули інтегрування детально розписані, тож хід інтегрування має бути зрозумілим.
ЗАВДАННЯ 5.10 Обчислити поверхневий інтеграл int(1+y+11z,ds) по поверхні сігма, де – частина площини x+y+z/3=1, що знаходиться в першому октанті
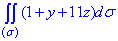
Розв'язання: Побудуємо площину x+y+z/3=1 лише в першому октанті та наведемо її проекцію в площину Oxy.
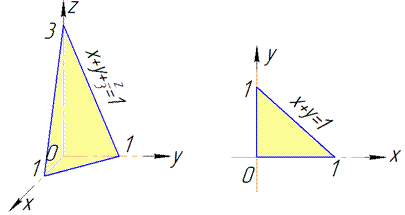
В усіх наведених тут прикладах проекція має вигляд прямокутного трикутника, дві сторони якого лежать на осях координат. Для таких областей інтегрування розставляти межі - просте заняття
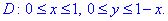
Для функції z=3-3x-3y знаходимо частинні похідні
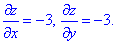
Підставляємо в диференціал поверхні та знаходимо коефіцієнт при dx*dy
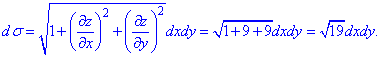
Перетворюємо поверхневий інтеграл до повторного та знаходимо його
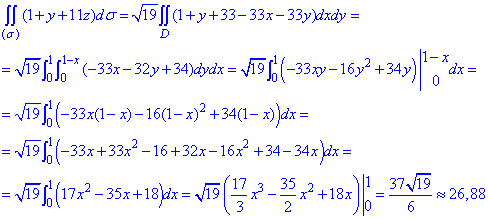
Інтегрувати функції не важко, тут не потрібно застосовувати заміни змінних чи інших хитрих прийомів для спрощення підінтегральних функцій.
ЗАВДАННЯ 5.12 Обчислити поверхневий інтеграл int(y-2z+4,ds) по поверхні 2x+y/3+z/4=1, що знаходиться в першому октанті
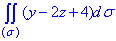
Розв'язання: Побудуємо площину sigma: 2x+y/3+z/4=1 та її проекцію.
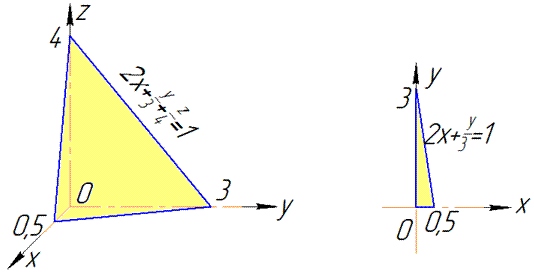
Тут і надалі площину будемо наводити тільки в першому октанті (чверті)
Задана площина в проекції в Oxy обмежена границями
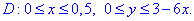
Обчислюємо частинні похідні функції поверхні z=4-8x-4/3*y за змінними
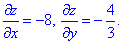
Далі визначаємо диференціал
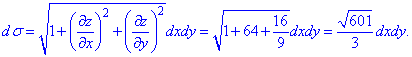
та підставляємо в поверхневий інтеграл
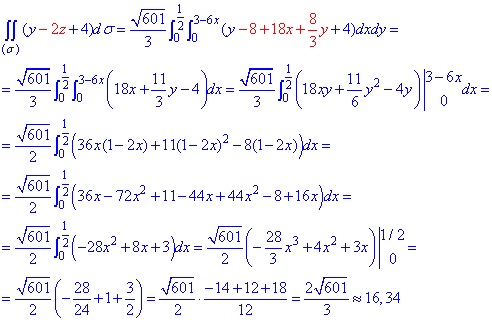
В формулі виписані всі розрахунки, включаючи підстановку меж.
ЗАВДАННЯ 5.14 Обчислити поверхневий інтеграл int(x+2z+2,ds) по поверхні sigma, де – частина площини x/2+y/3+z=1, що знаходиться в першому октанті
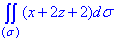
Розв'язання: Побудуємо площину інтегрування: x/2+y/3+z=1.
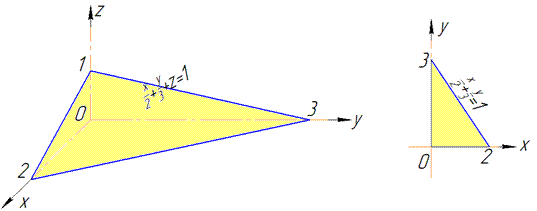
Бачимо, що задана площина проектується на область D в Oxy наступним чином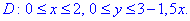 
Щоб обчислити поверхневий інтеграл І роду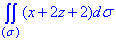 
виражаємо функцію z=1-x/2-y/3, тоді частинні похідні рівні
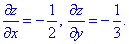
Знаходимо диференціал поверхні
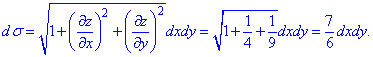
Застосовуємо формулу поверхневого інтегралу та виконуємо обчислення
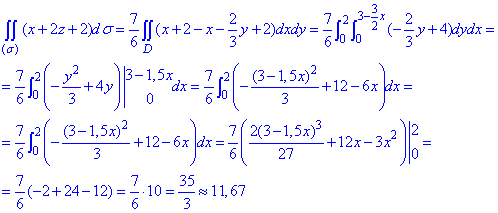
Як знайти подвійні інтеграли Ви вже знаєте з попередніх прикладів.
ЗАВДАННЯ 5.17 Обчислити поверхневий інтеграл int(x+2z+2,ds) по поверхні сігма, де – частина площини 2x+y/3+2z=1, що знаходиться в першому октанті
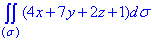
Розв'язання: Графік поверхні 2x+y/3+2z=1 та її проекції мають вигляд.
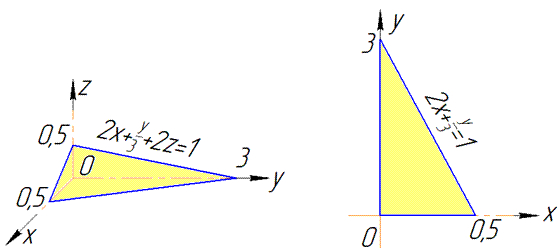
Ще раз нагадуємо, що це лише справедливо коли область обмежена першим октантом.
Проекція площини в Oxy дає наступні обмеження
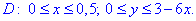
Нехай z=1/2-x-y/6, тоді частинні похідні приймають значення
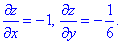
Обчислюємо диференціал
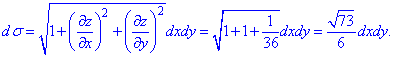
Переходимо від поверхневого інтегралу до повторного та знаходимо його значення
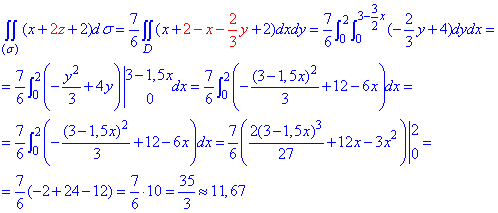
Інтегрувати не складно, розписуємо квадрати та повторно інтегруємо по аргументу.
ЗАВДАННЯ 5.17 Обчислити поверхневий інтеграл int(x+2z+2,ds) по поверхні , де – частина площини x/2+y/3+z=1, що знаходиться в першому октанті
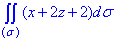
Розв'язання: Виконуємо побудову площини: x/2+y/3+z=1 в першому октанті.
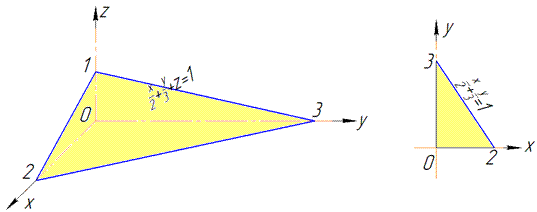
З графіку виписуємо проекцію області в площину Oxy
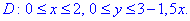
А далі все за схемою: для функції z=1-x/2-y/3 знайдемо похідні
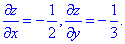
та підставимо у формулу диференціалу
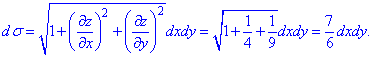
Поверхневий інтеграл І роду перетворюємо до кратного та обчислюємо
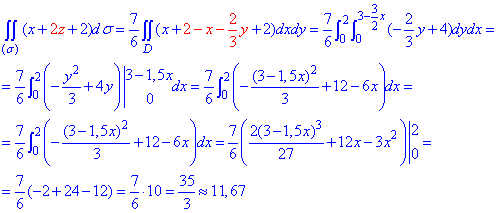
ЗАВДАННЯ 5.22 Обчислити поверхневий інтеграл int(x+2y-z+1,ds) по поверхні сігма:
x/4+y/2+z/3=1, де – частина площини, що знаходиться в першому октанті
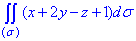
Розв'язання: Побудуємо площину: x/4+y/2+z/3=1 в першому октанті.
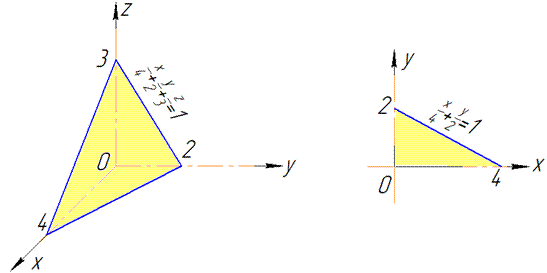
З рисунку бачимо, що проекція площини обмежена областю: xє[0;4], yє[0;2-0,5x].
Виражаємо змінну z=3-3x/4-3y/2, та обчислюємо часткові похідні
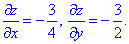
Далі знаходимо диференціал поверхні
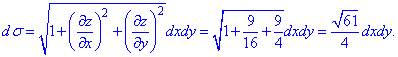
та поверхневий інтеграл
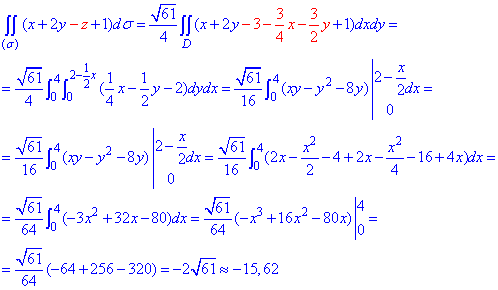
Формули та методика настільки розписані, що подібні завдання на контрольній чи екзамені Ви повинні вміти швидкао вирішувати.
Якщо ні - то у Вас великі проблеми з інтегруванням.
ЗАВДАННЯ 5.24 Обчислити поверхневий інтеграл int(7x+y+2z+2,ds)по поверхні , де – частина площини, що знаходиться в першому октанті
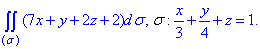
Розв'язання: Будуємо площину x/3+y/4+z=1 в першому октанті.
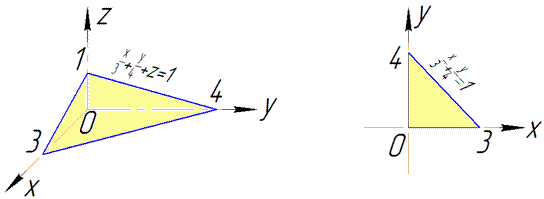
Описуємо проекцію площини в декартову множину Oxy
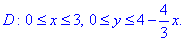
Знаходимо частинні похідні рівняння поверхні z=1-x/3-y/4
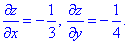
Підставляємо у формулу диференціала поверхні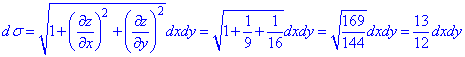 
Після спрощень обчислюємо поверхневий інтеграл
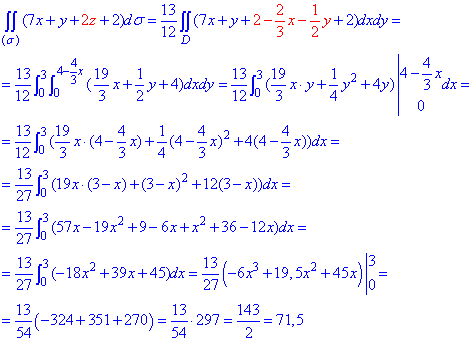
Формула не маленька, проте всі дрібні деталі добре розжовані.
Спробуйте це завдання виконати самостійно, а вкінці звірити відповіді.
ЗАВДАННЯ 5.25 Обчислити поверхневий інтеграл int(5x-2y+4z+1,ds) по поверхні , де – частина площини, що знаходиться в першому октанті
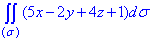
Розв'язання: Для наочності будуємо площину: x/2+4/y+z/3=1 та її проекцію.
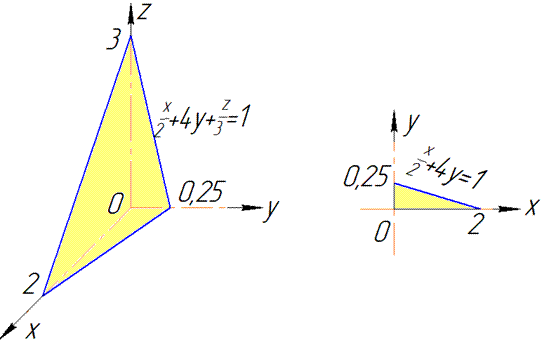
Записуємо межі області D в Oxy наступним чином
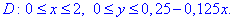
Для рівняння поверхні у вигляді z=3-3x/2-12y обчислюємо частинні похідні
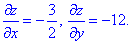
Знаходимо диференціал поверхні
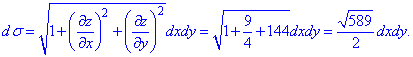
І найважче, що є у завданні - це обчислення поверхневого інтегралу через повторний
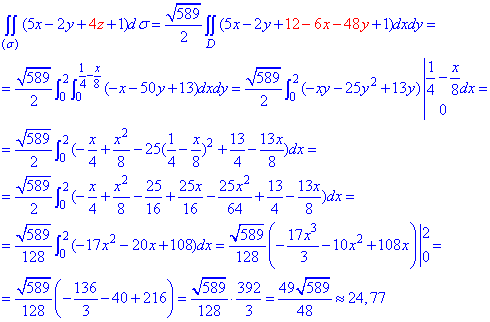
Тут найчастіше можна отримати помилку у відповіді через неправильне інтегрування, чи некоректну підстановку меж.
Більше задач на криволінійні інтеграли Ви можете знайти з сусідніх уроків.
