Наведемо готові відповіді до завдань на знаходження поверхневих інтегралів першого роду.
Усі приклади доповнені рисунками поверхонь по яких інтегруємо, пояснено для чого потрібна перша квадратична форма та коли вона потрібно. Алгоритм обчислення поверхневих інтегралів добре розписаний на різних параметризованих поверхнях, тож кількох прикладів Вам буде достатньо, що виконати контрольну чи розрахункову роботу!
Матеріал відповідає рівню підготовки студентів перших, других курсів ВУЗ-ів.
Завдання 1 Обчислити поверхневий інтеграл першого роду int[1/(1+x+y), S]
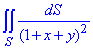
де S- межа тетраедра x+y+z≤1, x≥0, y≥0, z≥0.
Розв'язання: Перш ніж обчислювати інтеграл побудуємо схематичний вигляд тетраедра
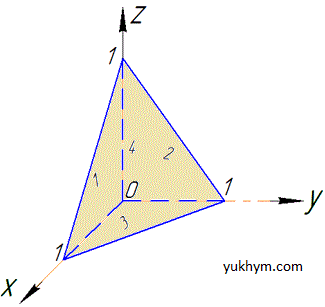
Заданий тетраедр складається з чотирьох площин (поверхонь), тому заданий поверхневий інтеграл рахуватимемо по всіх площинах окремо, тобто
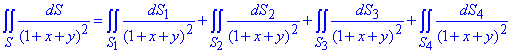
Поверхня 1: y=0.
Звідси, диференціал площі рівний dS1=dxdz.
Далі розставляємо межі 1-ї грані:
Враховуючи, що y=0 рівняння x+y+z=1 спроститься до вигляду x+z=1, звідси z=1-x верхня межа по z. Таким чином отримаємо
0≤x≤1 і 0≤z≤1-x.
Залишилося підставити y=0 в підінтегральну функцію та знайти поверхневий інтеграл першого роду
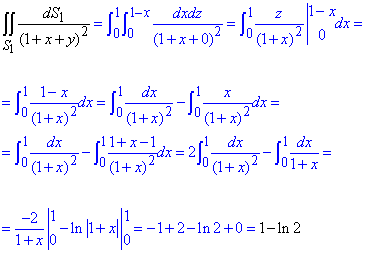 .
.
Далі аналогічні розрахунки для решти площин.
Поверхня 2: x=0.
Диференціал поверхні dS2=dydz, межі 2-ї грані:
0≤y≤1, 0≤z≤1-y.
Межі та підінтегральна функція змінюються з урахуванням умови x=0.
Обчислюємо кратний інтеграл
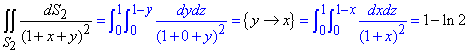
Поверхня 3: z=0.
Звідси, dS3=dxdy, а межі 3-ї грані:
0≤x≤1, 0≤y≤1-x.
Перевірте правильність наведених меж поверхневого інтеграла.
Наостанок, саме інтегрування
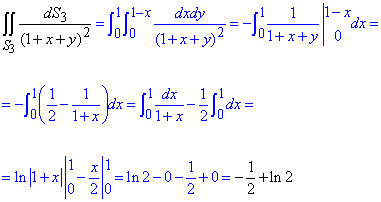
Поверхня №4: x+y+z=1.
На поверхні рівняння можемо переписати z=1-x-y, тому часткові похідні за двома іншими координатами від'ємні zx'=-1, zy'=-1.
Диференціал обчислюємо за формулою
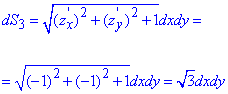
Межі 4 грані:
0≤x≤1, 0≤y≤1-x.
Обчислюємо ще один поверхневий інтеграл
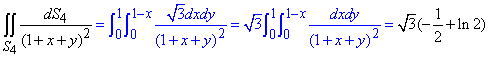
Кінцеве значення поверхневий інтеграл 1-го роду по гранях тетраедра знаходимо сумуванням знайдених значень: 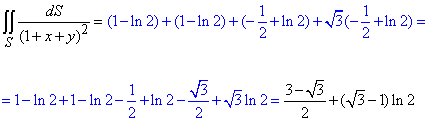
Подібним чином можна розраховувати поверхневий інтеграл по гранях будь-якого обмеженого площинами тіла.
Завдання 2 Обчислити поверхневий інтеграл першого роду int[x+y+z, S]
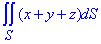
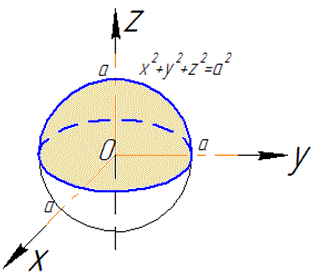
де S- поверхня сфери x2+y2+z2=a2, z ≥0.
Розв'язання: Маємо канонічне рівняння сфери в прямокутній системі координат.
Інтеграл потрібно знайти для верхньої його півкулі (див. рисунок)
Запишемо рівняння заданої сфери в параметричному вигляді: 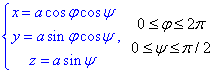
Ці формули є універсальними, тому їх часто будете використовувати для сферичних тіл. Кут "псі" відповідає за положення точок на сфері при z>0.
Для знаходження коефіцієнта І квадратичної форми потрібні похідні параметричного запису координат по обох кутах.
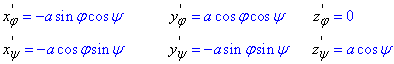
Обчислимо коефіцієнти І квадратичної форми за формулою: 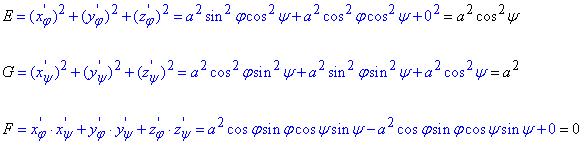
Формула першої квадратичної форми
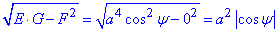
Вона слугує додатковим множник, який виникає внаслідок параметризації координат.
Поверхневий інтеграл першого роду знаходимо за формулою:
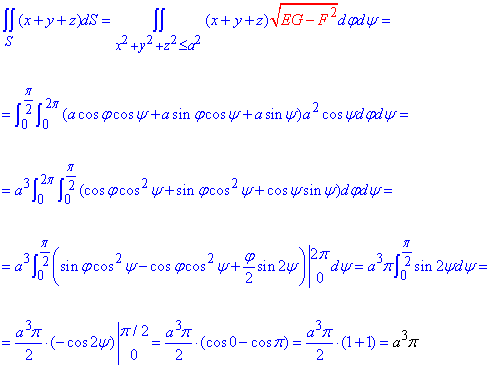
Уважно перегляньте інтегрування тригонометричних функцій. Тут деякі проміжні обчислення пропущені, це все для того, щоб спонукати Вас побільше працювати самостійно. З іншої сторони все що бачите слід перевіряти.
Завдання 3 Обчислити поверхневий інтеграл першого роду int[ z2, S]
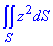
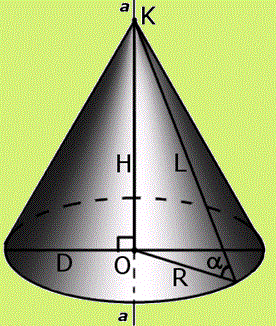
де S- частина поверхні конуса
x=r•cos(φ )sin(alpha),
y=r•sin(φ)sin(alpha),
z=r•cos(alpha)
(0≤r≤a; 0≤φ≤2π) і a- постійна, 0≤alpha≤π/2).
Розв'язання: Тут перший крок алгоритму обчислень поверхневого інтеграла пропускаємо, оскільки в умові вже маємо параметризоване рівняння конуса.
Знайдемо часткові похідні за кутом та радіус вектором
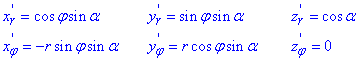
Далі за похідними обчислюємо коефіцієнти І квадратичної форми 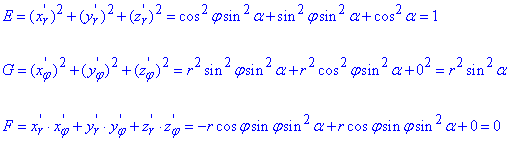
Поверхневий інтеграл першого роду обчислюємо за формулою 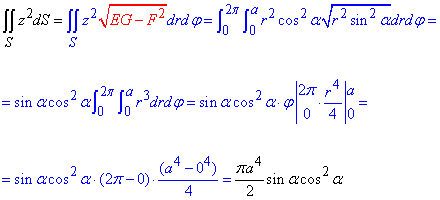
Спершу знаходимо внутрішній інтеграл за радіусом вектором, а далі за кутом "фі".
В результаті отримали, що поверхневий інтеграл залежить від кута при між площиною основи і твірною конуса - "альфа".
Більше прикладів на поверхневі інтеграли першого роду шукайте на сторінках сайту.
Добавляйте сайт в закладки та діліться посиланням на учбові матеріали з друзями!


