Розглянемо випадки коли області інтегрування симетричні відносно координатних осей та доцільно виконувати заміну змінних під інтегралом та переходити до полярних координат. Готові відповіді до прикладів на знаходження об'єму тіл через потрійний інтеграл покажуть наскільки така методика ефективна для перетинів куль, сфер, параболоїдів.
ЗАВДАННЯ 5.5
За допомогою потрійного інтеграла знайти об'єм тіла, що утворено поверхнями:
x2+y2+z2=4, x2+y2=3z.
Розв'язання: Проаналізуємо просторове тіло, що утворюється перетином заданих поверхонь.
x2+y2+z2=4 - куля з центром в початку координат O(0;0;0) і радіусом R=2,
x2+y2=3z - круговий параболоїд, що витягнутий вздовж осі Oz.
Знайдемо лінію перетину кулі та параболоїда:
для цього з рівняння кругового параболоїда суму квадратів змінних (праву сторону) підставимо в перше рівняння (рівняння кулі)
3z +z2=4, z2+3z=4, звідси z1=1 і z2=-4 (не задовільняє фізичній )
З рівняння слідує, що задані тіла перетинаються по колу:
x2+y2=3.
Розставимо межі інтегруванняz:
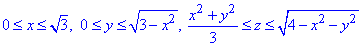
Тут взяли чверть тіла, тому результат помножили на четвірку.
Через потрійний інтеграл обчислюємо об'єм тіла
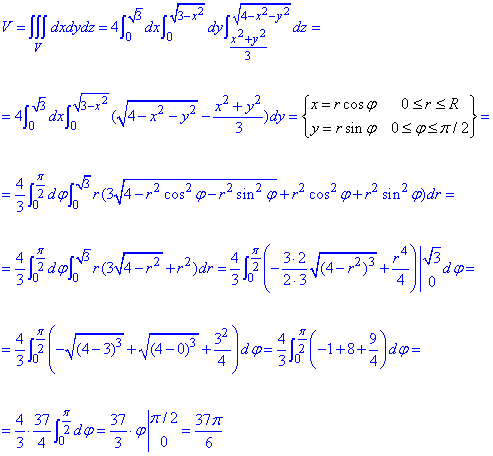
Всі важливі переходи при інтегруванні містить формула, тому добре розберіться з інтегралом.
ЗАВДАННЯ 5.6
За допомогою потрійного інтеграла знайти об'єм тіла, що утворено поверхнями:
x+y+z=0, x2+y2=1, z=0.
Розв'язання: Проаналізуємо форму тіла, що задана умовою:
x+y+z=0 - бісекторна площина,
x2+y2=1 - коловий циліндр, що витягнутий вздовж осі Oz.
Далі можемо розставити межі інтегралу:
0≤x≤1,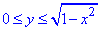 
, 0≤z≤-x-y,
Тут як і усіх симетричних тілах, беремо інтеграл у чверті тіла, а результат множимо на 4.
В результаті інтегрування знаходимо об'єм
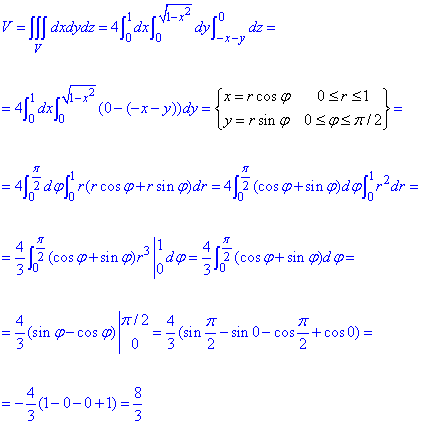
Тут, як і в попередньому прикладі, для спрощення обчислень під інтегралом робимо заміну змінних та переходимо до полярних координат.
На практиці це спрощує взяття інтегралів та спрощує розрахунок.
Запам'ятайте, що від вибору системи координат процес обчислення інтегралів має велике значення.
Кулі сфери, циліндри зручно інтегрувати в тих системах координат в яких їх канонічні рівняння мають найпростіший вигляд.
ЗАВДАННЯ 5.7
Знайти об'єм тіла, що утворено поверхнями:
z=2-18(x2+y2), z=2-44y
через потрійний інтеграл.
Розв'язання:
z=2-18(x2+y2) - еліптичний параболоїд, опущений вниз,
z=2-44y - площина, що паралельна осі Ox.
Знайдемо лінію перетину двох поверхонь:
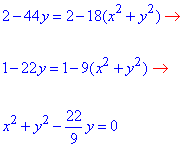
звідси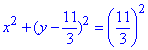 
- коло з центром у точці (0,11/3) і радіусом R=11/3.
Розставимо межі в заданій системі Oxz:
0≤x≤11/3,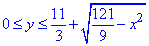 
, 2-44y≤z≤2-18(x2+y2),
Як і в попередніх прикладах взяли чверть тіла, тому результат помножимо на 4.
Обчислюємо потрійний інтеграл
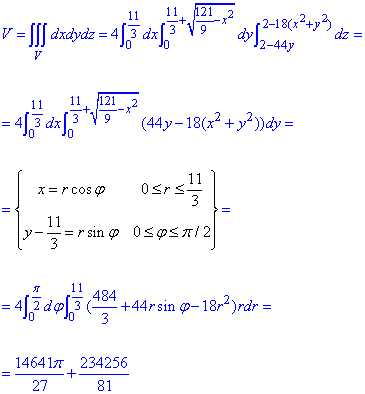
Інтегрування достатньо громіздке, тому тут наведені тільки основні результаті, до яких Ви повинні прийти. Ваш успіх залежить від вашого бажання працювати самостійно та кількості розв'язаних прикладів. Повірте, що легко не буде, але результат праці залишиться на довгі роки!
ЗАВДАННЯ 5.8
Використовуючи потрійний інтеграл знайти об'єм тіла, що утворене перетином поверхонь:
z=3√(x2+y2), z=10-x2-y2.
Розв'язання: Аналізуючи тримірні тіла робимо висновки, що задано:
z=3√(x2+y2)- верхня частина конуса.
z=10-x2-y2 - круговий параболоїд, що опущений вниз.
Співставленням рівнянь визначимо лінію перетину заданих поверхонь:
z2=9(x2+y2) і x2+y2=10-z, тоді
z2=9(10-z), z2+9z-90=0, звідси
z1=-15 (не задов.) і z2=6.
Отож, отримаємо коло x<suз> 22 з радіусом 2 і центром в початку координат.
Наступним кроком розставляємо межі в потрійному інтегралі:
0≤x≤2,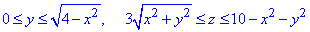 
Тут спростили, розглянувши чверть тіла, тому результат інтегрування множимо на 4.
Обчислюємо інтеграл
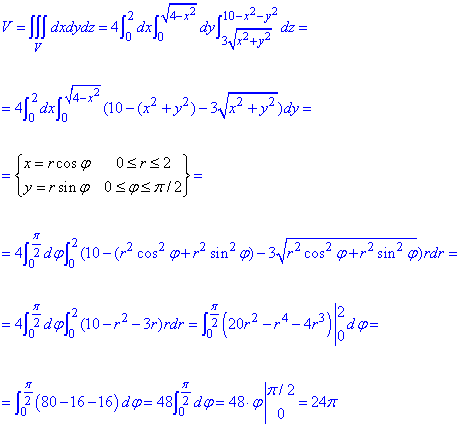
Об'єм тіла рівний 24π.
Не забувайте при переході до полярної системи координат домножувати підінтегральну функцію на якобіан, який рівний I=r.
Виведення формули чому рівний якобіан наведено в попередніх статтях. Ви лиш повинні знати, що без врахування цього множника Ви не отримаєте вірного результату, хоча виконаєте не менше обчислень ніж тут наведено.
Розбирайте наведені відповіді на знаходження об'ємів тіл через потрійний інтеграл і застосовуйте отримані знання настільки ефективно, щоб оформлення результатів у Вас виходило краще, аніж тут описано!
