Площа плоскої фігури. Подвійні інтеграли

Продовжуємо розбирати готові відповіді до завдань на обчислення площі плоских фігур через подвійні інтеграли.

ЗАВДАННЯ 4.5 Знайти площу плоскої фігури, що утворена лініями:
y²-2y-3x+1=0, 3x-3y-7=0.
Розв'язання: Проаналізуємо рівняння кривих, якими обмежена фігура.
y²-2y-3x+1=0, (y-1)²=3x - парабола з вершиною у точці (1;0) і гілками вправо.
3x-3y-7=0, y=x-7/3 - пряма.
Із системи рівнянь знайдемо точки перетину параболи з прямою:

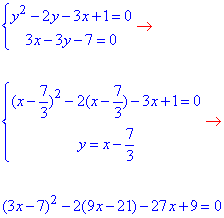
При розв'язуванні квадратного рівняння знаходимо "ікси", а далі з другого рівняння системи обчислюємо "ігрики".

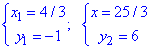
Графік фігури, площу якої шукаємо, наведено на рисунку

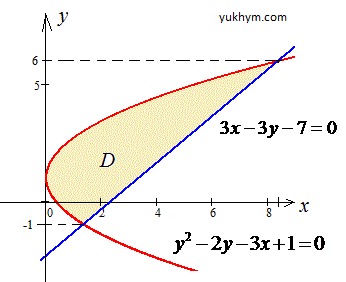
Розставимо межі в області D:
-1≤y≤6, ;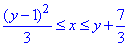
Знайдемо площу фігури через подвійний інтеграл:

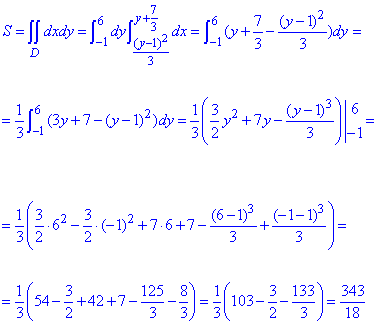
Уважно розберіть сам хід обчислень, це Вам допоможе на практичних.

ЗАВДАННЯ 4.6 Знайти площу плоскої фігури, що утворена лініями:
y=x, x=2y, x+y=3, x+3y=3.
Розв'язання: Всі задані лінії є прямими, отже фігура обмежена чотирикутником.
Складаємо системи рівнянь і знаходимо точки перетину різних пар прямих

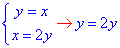
звідси x=0, y=0;

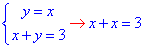
звідси x=1,5; y=1,5;

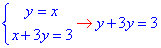
звідси x=0,75; y=0,75;

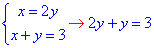
звідси x=2; y=1.
Графік прямих разом з чотирикутником наведено на рисунку

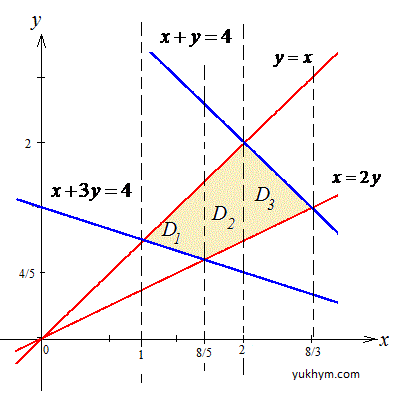
Щоб правильно знайти площу, область інтегрування D розіб'ємо на 3 (тут D=D1+D2+D3):
D₁: 3/4≤x≤6/5, 1-x/3≤y≤x;
D₂: 6/5≤x≤3/2, x/2≤y≤x;
D₃: 3/2≤x≤2, x/2≤y≤3-x.
Знаходимо площу фігури інтегруванням:

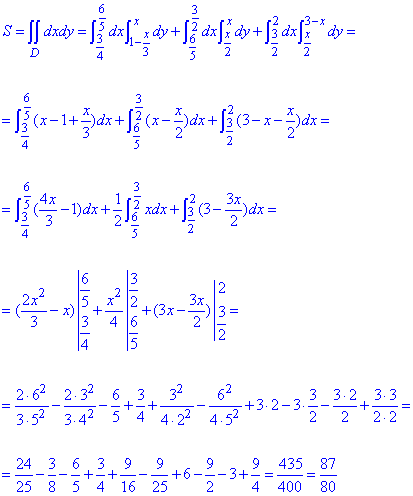
Обчислень багато, оскільки сумували зразу три інтеграли.
Площа рівна 87/80 одиниць квадратних.

ЗАВДАННЯ 4.7 Знайти площу плоскої фігури, що утворена лініями:
y²=12x, x+y=9, y=0.
Розв'язання: y²=12x - рівняння параболи з вершиною в початку координат і гілками вправо;
x+y=9, y=9-x - пряма, яка відтинається на осях у точках (9;0) і (0;9).
y=0 – вісь ординат.
Знайдемо точки перетину параболи з прямою:

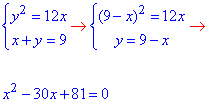
звідси

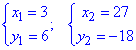
Друга точка нас не цікавить (y=0), оскільки ще маємо точку перетину двох прямих в точці (9;0) та параболи з прямою в початку координат (0;0).
Графік кривих наведено далі

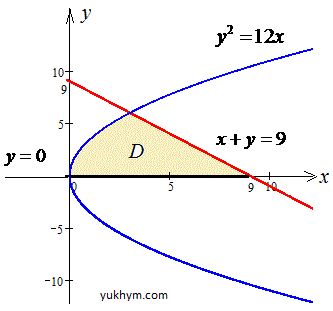
Розставимо межі в області D:
0≤y≤6, y^2/12≤x≤9-y.
Обчислюємо площу фігури через подвійний інтеграл:

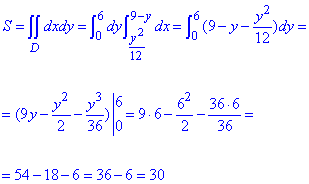
ЗАВДАННЯ 4.8 Знайти площу плоскої фігури, що утворена лініями:
x²+y²=16 (у плоскій фігурі координати z не повинно бути).
Розв'язання: Фігура є кругом радіусом 4. Його площу можна знайти за аналітичною формулою, але суть завдань навчити Вас обчислювати площу криволінійних поверхонь через інтеграли.

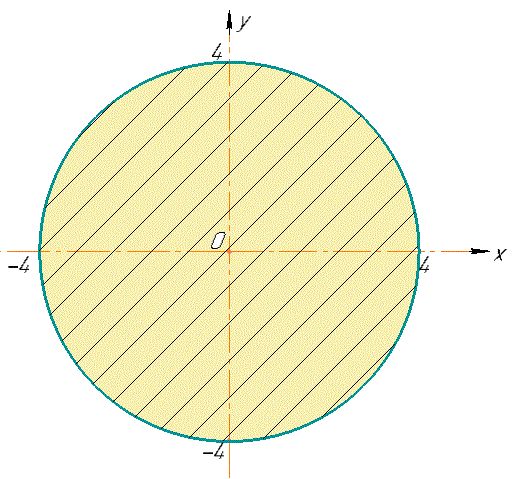
Кола найлегше інтегрувати в полярній системі координат, для цього використаємо формули:

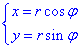
Знайдемо якобіан переходу:

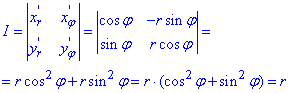
Запишемо задані криві в полярній системі координат:

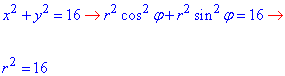
звідси маємо межі 0≤r≤4, 0≤φ≤2π.

Обчислюємо площу фігури через подвійний інтеграл:

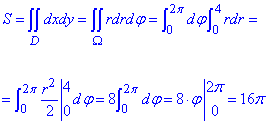
Площа рівна 16π одиниць квадратних.