Потрійний інтеграл. Об'єм тіла

Потрійні інтеграли мають широке застосування не тільки в математиці, з їх допомогою можна розрахувати об'єми складних тіл.
В студентській практиці все спрощується до тіл, які утворилися перетином сфер, параболоїдів, циліндрів з площинами, сферами і ін.
Вся суть знаходження об'єму тіл зводиться до правильного розставлення меж в потрійному інтегралі та швидкому інтегруванні.
Під правильним маємо на увазі, що багато з Вас вміють красиво малювати значок інтеграла, розставити та знайти межі можуть не всі, а от з інтегруванням справи ще веселіше.
Тому вчіть таблицю інтегралів та уважно читайте кожен рядок того, що ми тут написали, щоб Вас підтягнути!

ЗАВДАННЯ 5.1

За допомогою потрійного інтеграла знайти об'єм тіла, що утворено поверхнями:
x²+y²=16, z=0, z+y=2.
Розв'язання: Спершу аналізуємо чим обмежена просторова поверхня:
x²+y²=16- круговий циліндр,
z+y=2 - площина, яка паралельна осі Ox.
Межі інтегрування в заданій системі Oxz:
0≤x≤4, 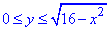, 0≤z≤2-y.
Тут і далі будемо брати тільки чверть тіла, оскільки усі тіла обертання симетричні.
Результат при цьому потрібно не забути помножити на 4.
Об'єм тіла записуємо через потрійний інтеграл, а далі виконуємо обчислення

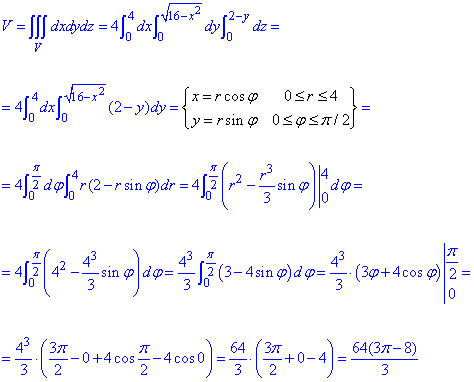
В окремих випадках доцільно перейти до полярних координат, при цьому слід підінтегральну функцію помножити на якобіан переходу I=r, що ми зробили.
І якщо цього вимагають, потрібно писати, що об'єм вимірюється в одиницях кубічних.
Це звичайно дрібничка, але іноді й на це звертають відповідь викладачі при оцінці оформлення відповідей.

ЗАВДАННЯ 5.2

За допомогою потрійного інтеграла знайти об'єм тіла, що утворено поверхнями:
z=x²+y², z=0, x²+y²=R², z≥0.
Розв'язання: Задано z=x²+y² - еліптичний параболоїд,
x²+y²=R² - коловий циліндр, що витягнутий вздовж осі Oz.
Графіки параболоїдів, гіперболоїдів є у відкритому інтернеті, тому окремо для цієї статті ми їх не робили.
Можливо, як буде вільний час, зробимо 3D рисунки заданих в умовах тіл через "gif" формат зображень.
Розставимо межі в проекції на площину Oxz:
0≤x≤R,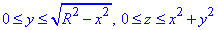
Знову розглядаємо лише чверть фігури, тому результат помножимо на 4.
Знаходимо об'єм тіла через потрійний інтеграл

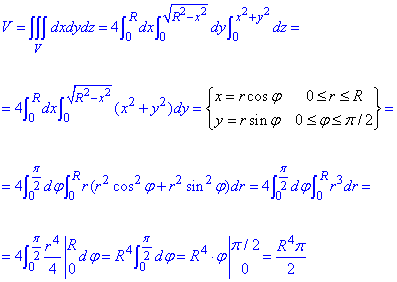
Самі обчислення коментувати немає сенсу, оскільки це велика тема і деколи на поясненні одного прикладу можна написати немалу статтю. Деталі переходу до полярних координат детально описані в категорії Інтегрування на цьому сайті, то ж розбирайте самостійно.

ЗАВДАННЯ 5.3

За допомогою потрійного інтеграла знайти об'єм тіла, що утворено поверхнями:
y²=z, x+y=2, x=0, z=0.

Розв'язання: Просторове тіло обмежене y²=z - параболічним циліндром, що витягнутий вздовж осі Ox;
x+y=2 - площиною, що паралельна осі Oz.
Розставляємо межі:
0≤x≤2, 0≤y≤2-x, -y²≤z≤y².
Деколи важко розставити межі й необхідно розбивати тіло на підобласті, або змінювати порядок інтегрування для спрощення кінцевого інтегрування.

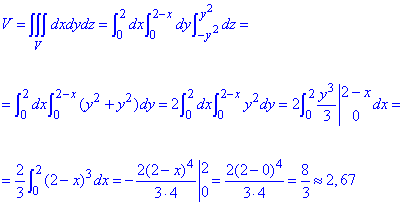
В цьому випадку взяти потрійний інтеграл достатньо просто, перехід до полярних координат є більш складним, тому розглянемо такі приклади.

ЗАВДАННЯ 5.4

За допомогою потрійного інтеграла знайти об'єм тіла, що утворено поверхнями:
x²+y²+z²=R², .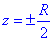

Розв'язання: Задане тіло обмежене x²+y²+z²=R²- кулею з центром в початку координат і радіусом R та
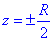- площинами, які відтинають кулю паралельно площині z=0 і є симетричними відносно неї.
Легко уявити собі, що лінією перетину будуть кола.
В силу симетрії межі інтегрування випишемо лише для першої чверті
0≤x≤R, ,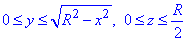
а результат помножимо на 4.

Всередині інтегрування переходимо до полярних координат та знаходимо об'єм заданого тіла

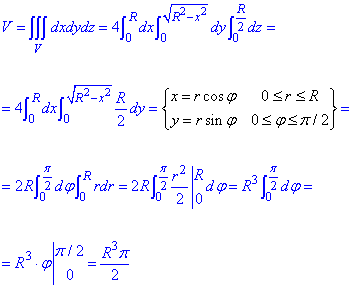
Уважно перегляньте як виконується перехід до полярної системи під інтегралом, враховується якобіан та саме інтегрування. На першому, другому курсі у ВУЗах такі приклади досить поширені. Далі розглянемо, ще кілька завдань на знаходження об'єму інтегруванням.