Несвойственный интеграл I рода
Если функция f(x) интегрирована за Риманом на каждом конечном промежутке [a;b], тогда несвойственный интеграл находят через предельный переход за формулой
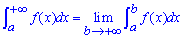
и говорят, что несвойственный интеграл совпадающий, если существует такая конечная граница.
В противном случае (если граница бесконечна или не существует) говорят, что интеграл разбегается.
Несвойственный интеграл ІІ рода
Если функция f(x) неограничена в околе точки B и интегрирована за Риманом на каждом конечном промежутке 
, тогда несвойственный интеграл ІІ рода вычисляют по формуле
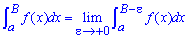
и говорят, что интеграл совпадающий, если существует его конечная граница. В противном случае (если граница бесконечна или не существует) говорят, что интеграл разбегается. Точка B называется особенной.
І. Вычислить интегралы
Начнем рассмотрение готовых ответов к несвойственным интегралам от простых к сложным заданиям.
Пример 2.147 (2334) Найти несвойственный интеграл
Имеем несвойственный интеграл І роду. Изменяем бесконечность на фиксированную точку из промежутка, вычисляем интеграл и после подстановки пределов интегрирования находим границу при следовании верхнего предела к бесконечности
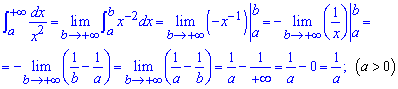
Пример 2.148 ( 2335) Найти интеграл
Подинтегральная функция (логарифм) неопределенна в нуле, который отвечает нижней границе интегрирования. В соответствии с вышеприведенными формулами, имеем несвойственный интеграл второго рода. Для его нахождения переходим к границе в нуле, также выполняем интегрирование частями
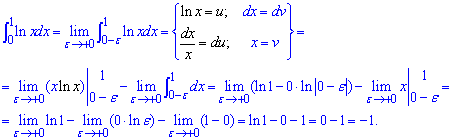
Сам по себе интеграл не сложен в плане вычислений.
Замечание: в дальнейшем границу писать НЕ будем, а при вычисление несвойственных интегралов понимаем, что ищем значения границы в особенных точках (или в плюс минус бесконечности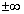 
) !!!
Пример 2.149 (2336) Вычислить интеграл
Разбиваем интеграл на 2 и находим несвойственные интегралы І рода
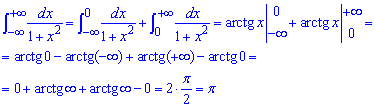
Пример 2.150 (2337 ) Найти интеграл
Выполняем манипуляции идентичные, как и в предыдущем задании и приходим к несвойственным интегралам второго рода
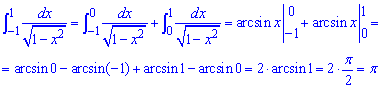
Пример 2.151 ( 2338) Найти интеграл
Верхняя граница направляется к бесконечности, следовательно имеем несвойственный интеграл первого рода. Для нахождения предельного значения находим неопределенный интеграл и при подстановке пределов выносим переменную за скобки в числителе и знаменателе логарифма. В результате вклад бесконечно малых величин (1/x) направляется к нулю при переменной направляющейся к бесконечности. Таким образом находим главное значение интеграла
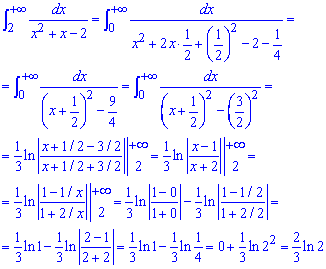
Пример 2.152 (2339) Найти интеграл
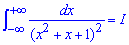
Решение: Вычислим последний интеграл методом Остроградського - метод не из простых, однако эффективный в подобных примерах:
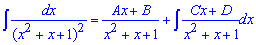
возьмем производную от каждой части равенства (производная от интеграла равная подинтегральной функции)
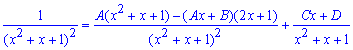
Возведем дроби в правой части равенства к общему знаменателю и приравняем коэффициенты при соответствующих степенях x каждой части равенства
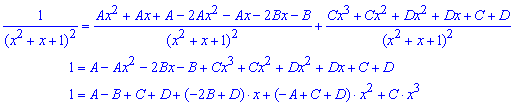
В результате получим систему из 4 линейных уравнений из которой находим 4 константы
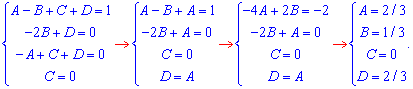
Таким образом можем записать неопределенный интеграл в виде
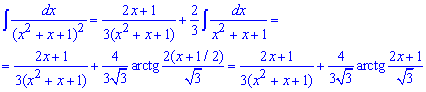
Дальше подставляем пределы и находим границе дроби и арктангенса при переменной направляющейся к плюс минус бесконечности.
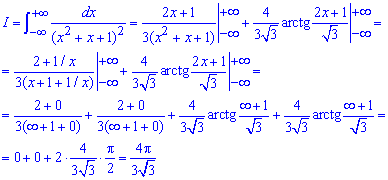
В конечной формуле можно еще избавиться от иррациональности в знаменателе, но это уже проделайте самостоятельно.
Пример 2.153 ( 2340)Найти интеграл
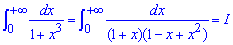
Вычислим последний интеграл методом неопределенных коэффициентов:
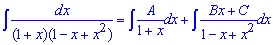
Записываем подинтегральные функции и, возведя их под общий знаменатель,
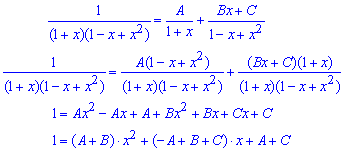
а дальше приравняем коэффициенты при соответствующих степенях x каждой части равенства.
В результате решим систему трех уравнений и определим сталые
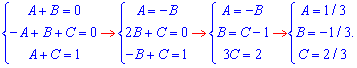
Подставим их в расписание и найдем неопределенный интеграл
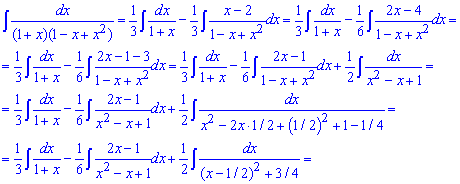
после возведения под табличные формулы интегрирования получим логарифмы, которые группируем и арктангенс.
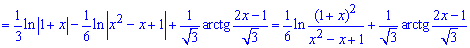
В бесконечности выносим из числителя и знаменателя дроби под логарифмом слагаемое с самым старшим показателем переменной и сокращаем на него. Тогда получим логарифм единицы.
В нуле с точностью до наоборот, сталые оставляем - остальные слагаемые с переменными не дают вклада.
С арктангенсом ситуация более определена и его значение на пределе подставляем в формулу
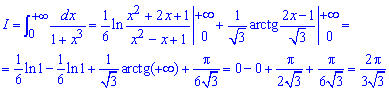
Пример 2.154 ( 2341)Вычислить интеграл
Покажем, как можно найти интеграл такого вида двумя способами.
І способ: расписание методом неопределенных коэффициентов:
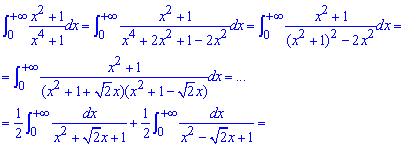
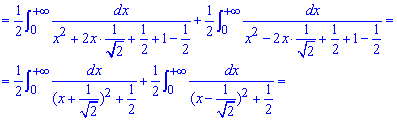
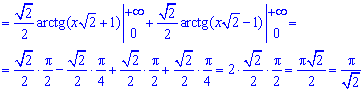
Чему равен арктангенс в нуле, единице и бесконечности Вы должны знать на память при решении подобных заданий.
Здесь применили метод неопределенных коэффициентов (A=C=0; B=D=1/2) :
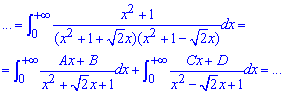
ІІ способ - через замену переменных:
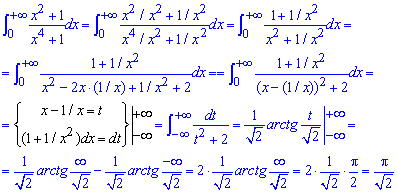
Пределы интегрирования при замене переменных здесь стали другими (в нуле минус бесконечность).
Пример 2.155 (2342) Найти интеграл
Особенной точкой здесь является нуль, поскольку корень в знаменателе становится равным нулю, а подинтегральная функция направляется к бесконечности. Но это происходит на таком малом участке интегрирования, что вклад мизерен и в целом интеграл совпадающий.
Для его вычисления переходим под интегралом к новым переменным, находим новые пределы интегрирования и находим арктангенсы на краях
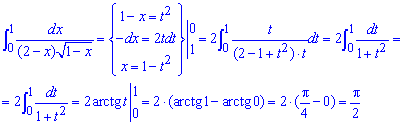
Вычисления не сложны, поскольку свели интегрирование под простой табличный интеграл.
Пример 2.156 (2343) Найти интеграл
В бесконечности подинтегральная функция направляется к нулю, поэтому делаем вывод, что имеем несвойственный интеграл І рода. Для его нахождения кое-как превращаем функцию и выполняем замену переменных
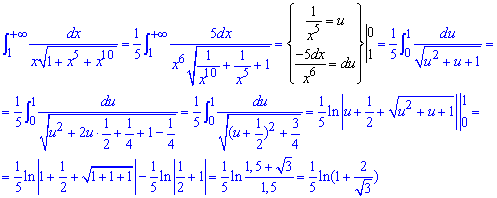
В результате сводим интеграл к логарифму, который упрощаем используя свойства логарифмов.
Пример 2.157 ( 2344) Найти интеграл
Имеем несвойственный интеграл І рода. Выполняем интегрирование частями
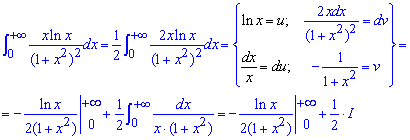
Второе слагаемое раскладываем методом неопределенных коэффициентов
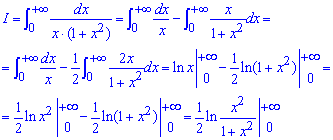
В результате приходим к случаю когда имеем несвойственный интеграл І и ІІ рода одновременно, поэтому предел будет иметь вид
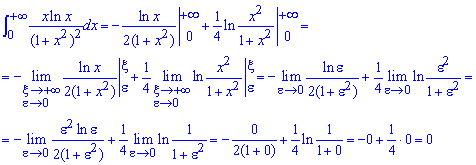
Здесь учтены следующие предельные переходы
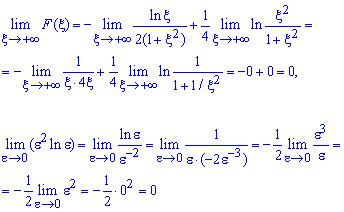
Интеграл равен нулю.
Пример 2.158 (2345) Вычислить интеграл
В бесконечности подинтеграьная функция направляется к нулю - имеем І несвойственный интеграл.
Обозначив арктансенс через новую переменную определяем пределы интегрирования, дальше упрощаем функцию и интегрированием частями находим значение в крайних точках.
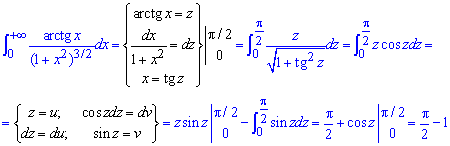
Пример 2.159 (2346) Найти интеграл
Неопределенный интеграл І рода решаем дважды применив интегрирование частями
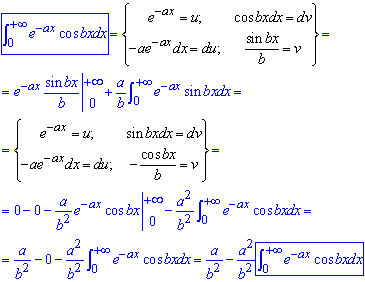
В результате приходим к записи интеграла через самого себя, то есть рекуррентной формуле
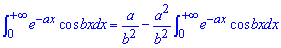
Перегруппировываем известные и неизвестные по разные стороны знака равенства
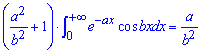
и выражаем
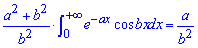
отсюда искомый интеграл
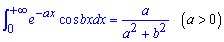
Метод не новый, и когда Вы имеете произведение экспоненты на синусы и косинусы без него не обойтись.
Пример 2.160 ( 2347) Найти интеграл
На бесконечности подынтегральное выражение дает бесконечно малую осциллирующую около нуля функцию.
Чтобы обойти такую неопределенность используем методику предыдущего примера. Дважды применив интегрирование частями
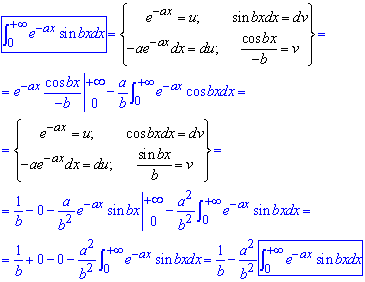
приходим к рекуррентной формуле
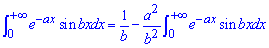
Из нее найти интеграл достаточно просто:
интегралы переносим в одну сторону, сталые в другую.
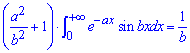
А дальше выполняем деления одной постоянной справа на множитель при интеграле
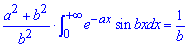
Отсюда и имеем искомый интеграл
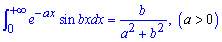
Запомните методику последних двух заданий, на модулях и экзаменах на этом поплатилась значительная часть студентов.
Не будьте в их числе!
Пример 2.161 Найти интеграл
Имеем несвойственный интеграл І рода. Находим его и делаем вывод
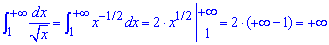
что интеграл разбегается, поскольку преде не является конечным.
Пример 2.162 Найти интеграл
Экспоненту интегрировать не трудно, при отрицательном показателе она в бесконечности направляется к нулю
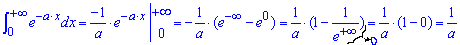
Пример 2.163 Вычислить интеграл
Интеграл по виду не сложный, однако при подстановке пределов многие из Вас пишут логарифм минус логарифм = бесконечность минус бесконечность, а дальше что границы не существует, а интеграл расходится.
А он совпадающий причем к нулю
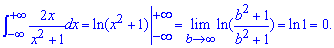
В этом также легко убедиться проанализировав подинтегральную функцию, ее знаменатель положительный для положительных и отрицательных значений переменной, числитель непарная функция, следовательно интеграл справа от оси абсцисс нивелирует интеграл слева.
Пример 2.164 Найти интеграл
В знаменателе дроби выделяем полный квадрат и сводим интеграл под формулу арктангенса.
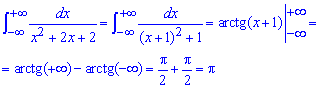
При следовании переменной к бесконечности арктангенс направляется к Pi/2, при минус бесконечности к - Pi/2.
В сумме получаем Int=Pi.
Пример 2.165 Найти интеграл
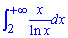
Имеем интеграл І рода. Покажем, что он расходится. Знаменатель на рассматриваемом промежутке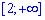 
удовлетворяет условие ln(x)<x-1, поэтому имеем следующее неравенство между функциями
,
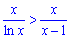Однако второй интеграл расходится
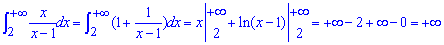
Поскольку функция принимает большие значения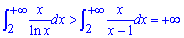 
, то заданный интеграл 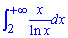также расходится!
Пример 2.166 Найти интеграл
Имеем несвойственный интеграл І рода. Его находим расписанием подинтегральной функции через простые множители, как это реализовать расписано дальше
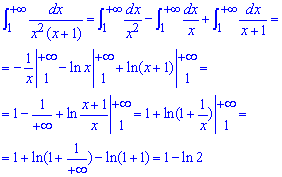
Данный интеграл нашли методом неопределенных коэффициентов:
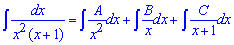
записываем функцию в виде расписания простых дробей
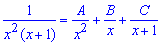
Дальше их возводим к общему знаменателю
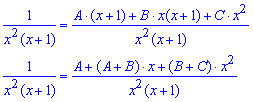
приравняем коэффициенты при соответствующих степенях x в обеих частях равенства и находим сталіе A=1, B=-1; C=1 .
Их и подставляем в интеграл
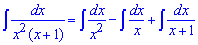
Пример 2.167 Найти интеграл
Чтобы не раскладывать на простые дроби через неопределенные коэффициенты прибавим и отнимем в числителе единицу. Это позволит получить в числителе такой же множитель как и знаменатель и разложить дробь на два интегралы.
Дальнейшее их вычисление и определение пределов приведено в формуле
.
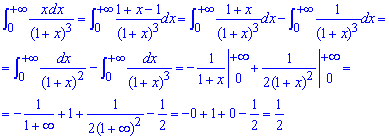Пример 2.168 Найти интеграл
При переменной направляющейся к бесконечности функция, которая интегрируется направляется к нулю. Имеем несвойственный интеграл первого рода. Чтобы найти его значение выносим переменную из под корня знаменателя, переходим к новой переменной интегрирование (при этом изменяются пределы). В результате получим арксинус, который и вычисляем
.
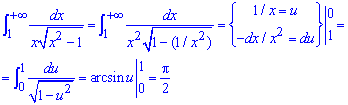Пример 2.169 Найти интеграл
Здесь необходимо, чтобы параметр превращался в нуль. Для других его значений несвойственный интеграл первого рода находим методом замены переменных. В результате приходим к логарифму, который расписываем к самому простому виду
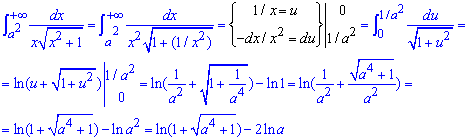
Пример 2.170 Найти интеграл
Здесь в нуле надо найти предел, для этого вычисляем несвойственный интеграл, и подставляем пределы интегрирования.
Интеграл равен 0,5.
Пример 2.171 Найти интеграл
В нуле имеем особенность, которую при интегрировании необходимо обойти. Сначала превращаем функцию, чтобы перейти к новой переменной. Дальше применяем интегрирование частями, если множителем имеем экспоненту то это быстро приводит к конечному результату или рекуррентной формуле. Дальше подставляем пределы и анализируем, какие слагаемые сбегаются и к какой границе (значении).
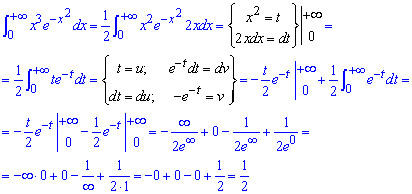
Пример 2.172 Найти интеграл
В бесконечности синус осциллирует, если умножить на переменную то получим осциллирующую функцию с растущей амплитудой. Выполняем интегрирование частями и переходим к границе.
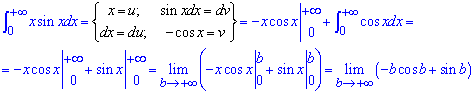
Поскольку последней границы не существует, то интеграл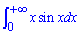 
расходится.
Пример 2.173 Вычислить интеграл
Поскольку мы знаем к чему сводить подобные интегралы, то выполняем превращение функции в начале. Вы же можете обозначить корень из аргумента за новую переменную и в результате превращений прийти к тому же конечного интегралу. Самостоятельно проинтегрирував частями, Вы получите, что интеграл равен единице
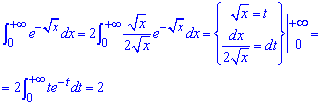
Пример 2.174 Найти интеграл
В подобных примерах нужно дважды применять интегрирование частями.
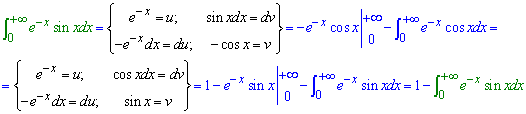
В результате придем к рекуррентной формуле
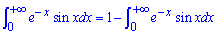
откуда и определяем интеграл
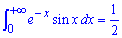
Данный интеграл - это классика интегрирования, если бы экспонента и синус имели множители при аргументах, то вычисления были не такие простые как в рассмотреном примере.
Пример 2.175 Найти интеграл
Здесь с первого взгляда может показаться, что интеграл не принадлежит к несвойственным. Однако, разложив знаменатель на одночлены, видим, что во внутренней точке имеет особенность, а именно разрыв второго рода.
При нахождении несвойственного интегралу второго рода при переходе к границам два логарифма упрощаем, по правилу разница логарифмов равна логарифму части. Таким образом лишь одно из слагаемых дает вклад
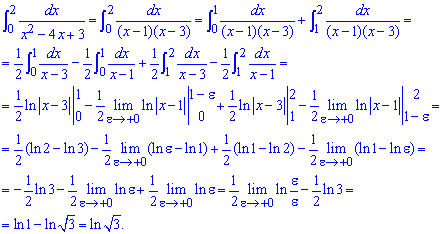
На графике функции эта особенность имеет вид
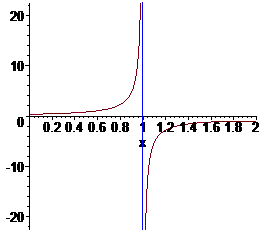
Пример 2.176 Найти интеграл
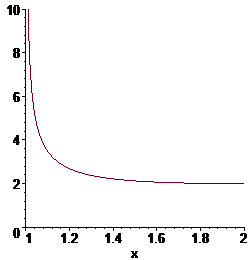
В единице корень в знаменателе превращается в нуль и функция там имеет вертикальную асимптоту. Чтобы ее обойти прибавим и отнимем в числителе единицы и распишем интеграл на два. Их вычисление уже не содержит никаких особенностей
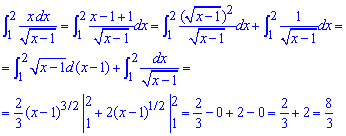
График функции, не доходя до 1 справа имеет вид
Пример 2.177 Найти интеграл
Неопределенность в заданный интеграл вносит то что логарифм вблизи нуля направляется к минус бесконечности. Интегрируя частями, придем к особенности в нуле, Вы ее можете свести к следствию второй важной границы, мы же записываем конечное значение.
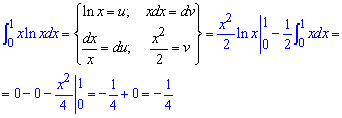
Для наглядности графики подинтегральной функции на указанном промежутке имеет вид
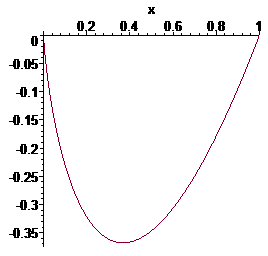
Как можно убедиться здесь все гладко и красиво.
Пример 2.178 Найти интеграл
При приближении к нулю за счет квадрата знаменателя функция растет к бесконечности. Но и при этом промежуток на котором это происходит направляется к нулю. Поэтому несвойственный интеграл существует и с помощью приведенной замены переменных находится без проблем
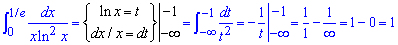
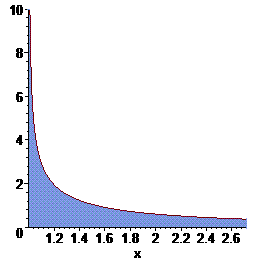
Найденный интеграл не что другое как площадь фигуры между функцией и осью ординат. За исключением особенности в нуле графики функции имеет вид верхней линии, а значение интеграла - заштрихованной на рисунке поверхности.
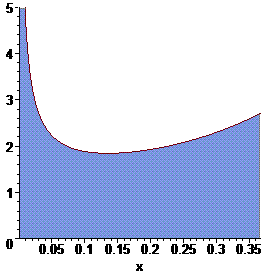
Пример 2.179 Найти интеграл
В единице логарифм направляется к минус бесконечности, чтобы учесть это выполняем замену переменных под интегралом
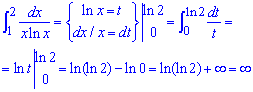
В результате предел равен бесконечности, поэтому заданный интеграл разбегается.
График подинтегральной функции в околі особенной точки имеет вид
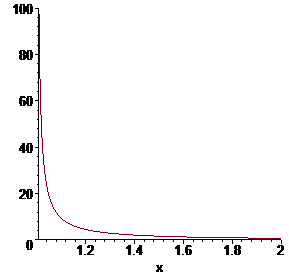
Пример 2.180 Найти интеграл
При приближении к единице логарифм направляется к нулю, а функция к плюс бесконечности.
Чтобы вычислить несвойственный интеграл ІІ рода выполняем замену переменных и переходим к корневой функции в знаменателе, которая после интегрирования не имеет особенности
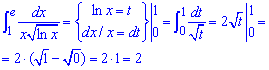
Значение интеграла равно площади заштрихованной фигуры.
Пример 2.181 Найти интеграл
Здесь свой вклад вносит точка x=0, поскольку в ней функция из двух сторон направляется к плюс бесконечности.
Разделим числитель на знаменатель и перепишем функцию в виде показателей переменной.
Дальше разделяем интеграл на два и находим значение в пределе.
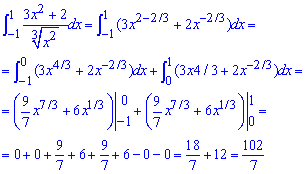
Получили совпадающий интеграл. Вид функции приведен на рисунку
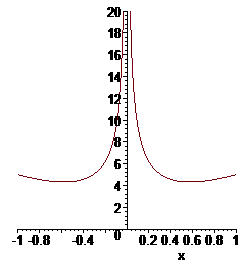
Пример 2.182 Найти интеграл
Здесь идентичная ситуация, в нуле имеем особенность. По схеме предыдущего задания находим два неопределенных интеграла
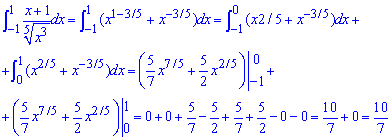
Пример 2.183 Найти интеграл
Здесь в нуле имеем особенность, но поскольку знаменатель в нуле непарный то график общей функции имеет в нуле разрыв второго рода. Такие функции интегрируемые и по схеме выше находим предел в нуле.
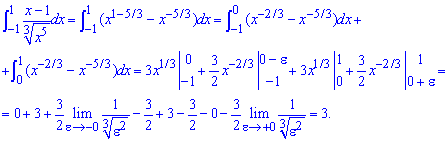
Около нуля график функции имеет вид
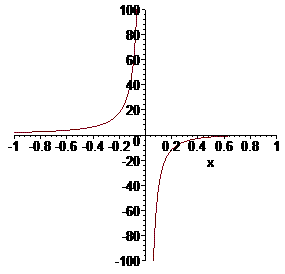
Пример 2.184 (2348) Найти интеграл
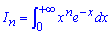
Вычислим нулевое приближение с устранимой особенностью в бесконечности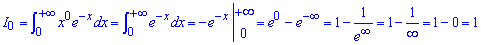
Дальше интегрированием частями находим значение для номера n
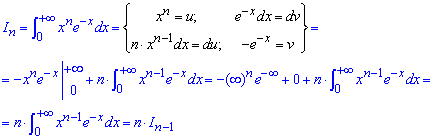
Получили рекуррентную формулу: In=n*In - 1, отсюда интеграл равен
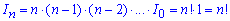
На этом ознакомление с основными приемами нахождения несвойственных интегралов подходит к концу.
Больше готовых ответов на интегрирование функций ищите на страницах сайта.
Если нужна помощь, также обращайтесь!
