Інтеграл другого роду вздовж кривої

Завдання 1 Обчислити криволінійний інтеграл 2-го роду int[(x2-2xy)dx+(y2-2xy)dy, C] вздовж кривих, що пробігають у напрямку зростання параметра:

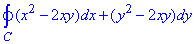
де C - парабола y=x² (-1≤x≤1).

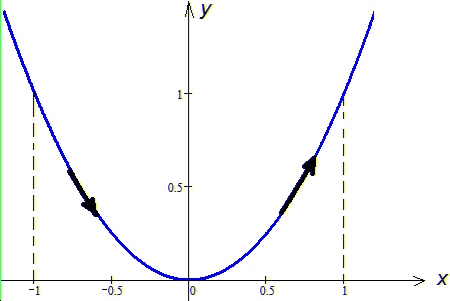
Розв'язання: Маємо параболу y=x² з вершиною в точці (0,0) і гілками вгору.
Графік параболи та напрямок обходу дуги наведено на рисунку

 Запишемо диференціал по змінній x від функції y=x²:
dy=2x•dx.
Обчислимо криволінійний інтеграл 2-го роду на проміжку -1≤x≤1:

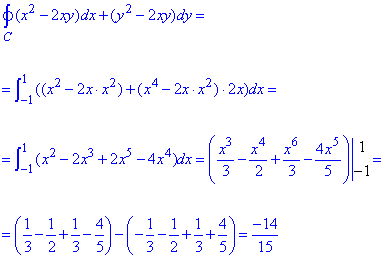
Інтеграл доволі легко обчислити. Загалом інтегрувати вздовж парабол, прямих, гладких функцій не важко, виняток складають приклади де маємо складні підінтегральні функції.

Завдання 2 Обчислити криволінійний інтеграл 2-го роду int[((x+y)dx-(x-y)dy)/(x²+y²), C)
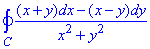вздовж кола, де C - коло x²+y²=a², що пробігається проти ходу годинникової стрілки.

Розв'язання: Маємо коло з центром в початку координат та радіусом R=a.

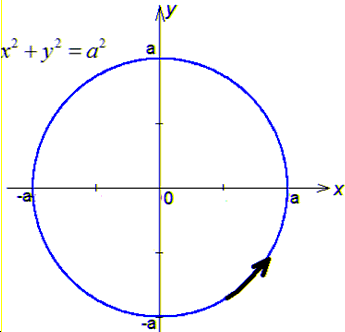
 Перейдемо до полярної системи координат за допомогою формул переходу: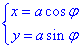
де 0≤φ≤2π.
Знайдемо диференціали по куту φ від функцій x=x(φ) та y=y(φ):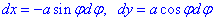
Обчислимо криволінійний інтеграл 2-го роду вздовж кола:

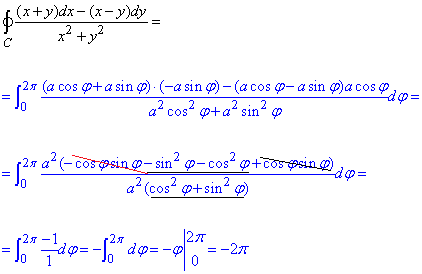
Вираз під інтегралом складений так, що в полярній системі координат підінтегральна функція спростилася до сталої.
Як Ви знаєте, інтеграл від сталої рівний змінній, далі підставляємо межі.

Завдання 3 Обчислити криволінійний інтеграл 2-го роду int[arctg(y/x)dy-dx, S] вздовж кривих, що пробігають у напрямку зростання параметра:

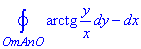
де OmA - дуга параболи y=x² і OnA - відрізок прямої y=x.

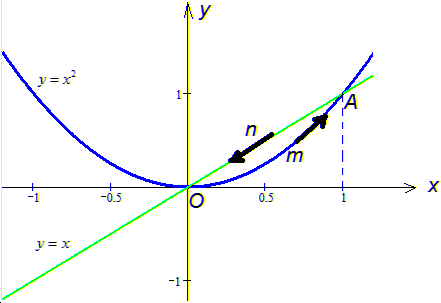
Розв'язання: OmA: маємо дугу параболи y=x² з вершиною в точці (0,1) і гілками вгору;
dy=2xdx, 0≤x≤1.
AnO: відрізок прямої y=x, яка перетинає параболу y=x² в точках (0,0) і (1,1);
dy=dx, 0≤x≤1.
Графік кривих вздовж яких будемо обчислювати криволінійний інтеграл наведено на рисунку:

Обчислимо криволінійний інтеграл 2-го роду на проміжках через суму інтегралів:

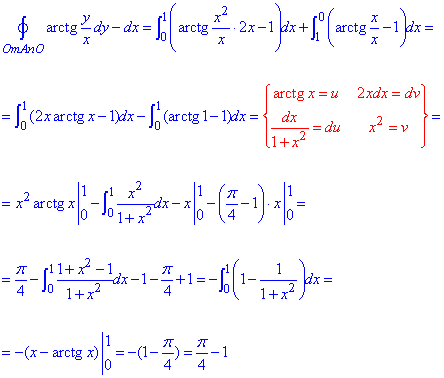
При знаходженні інтегралу виконали заміну змінних u=arctg(x), 2xdx=dv  та інтегрування частинами.
Без цього інтеграл Ви б не знайшли.
Залишайтеся з нами та вивчайте нове для себе.