Формула Остроградського-Гауса применяют для преобразования объемного (тройного) интеграла к интегралу по замкнутой поверхности (двойного), превращения объемного (тройного) интеграла к интегралу по замкнутой поверхности (двойного), и наоборот:
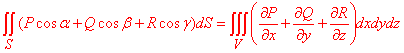
Другое приложение формулы это вычисления потока векторного поля через замкнутую поверхность с помощью интеграла от дивергенции этого поля по объему, что ограничен этой поверхностью.
Дальше будут приведены примеры перехода от двойного к тройному интегралу, расстановки пределов и вычисления объемных интегралов.
Пример 1 Используя формулу Остроградського-Гауса, превратить поверхностный интеграл
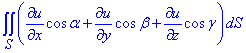
если гладкая поверхность S ограничивает конечный объем V и 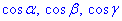 - направляющие косинусы внешней нормали к поверхности S.
- направляющие косинусы внешней нормали к поверхности S.
Решение: Поверхностный интеграл 2-го рода сводится к тройному интегралу с помощью формулы Остроградського-Гауса:
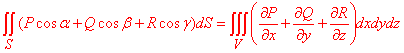
где P, Q, R выписываем из заданного интеграла
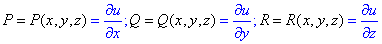 - частичные производные функции.
- частичные производные функции.
Далее повторно вычисляем производные, чтобы получить направляющие косинусы в направлении каждой из осей
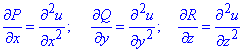
Можем перейти от двойного интеграла к тройному
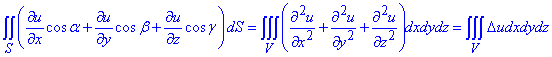
здесь обозначили Δu - дельта оператор Лапласа
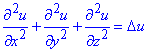
На этом все объяснения к первому примеру.
Пример 2 Используя формулу Гауса-Остроградського, превратить поверхностный интеграл
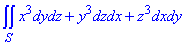
по гладкой поверхности S ограничивающей конечный объем V и 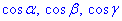 - направляющие косинусы внешней нормали к поверхности S.
- направляющие косинусы внешней нормали к поверхности S.
Решение: Поверхностный интеграл второго рода сведем к трехмерному интегралу, используя формулы Гауса-Остроградського:
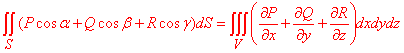
где P=P(x, y, z)=x3, P=P(x, y, z)=y3, P=P(x, y, z)=z3 берем из условия.
Вычисляем вторые производные по "икс, игрек, зет"
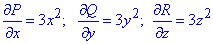
Записываем формулу перехода от двойного интеграла к тройному
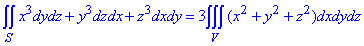
На этом примере Вы видите, что сам переход между кратными и тройными интегралами найти не трудно.
Значительное количество ждет при необходимости расставить пределы интегрирования и найти тройной интеграл.
Пример 3 Используя формулу Гауса-Остроградського, превратить поверхностный интеграл
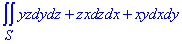
если гладкая поверхность S ограничивает конечный объем V и 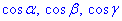 - направляющие косинусы внешней нормали к поверхности S.
- направляющие косинусы внешней нормали к поверхности S.
Решение: Поверхностный интеграл второго рода сведем к тройному интегралу, используя формулу Гауса-Остроградського : 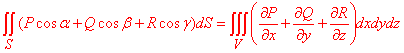
где P=P(x, y, z)=yz, Q=Q(x, y, z)=xz, R=R(x, y, z)=xy.
Частичные производные второго порядка от P, Q, R
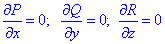
Поэтому тройной интеграл равен нулю
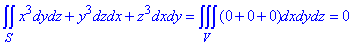
Пример 4 Используя формулу Гауса-Остроградського, вычислить поверхностный интеграл int[x3dydz+y3dzdx+z3dxdy, S]
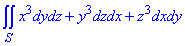
где S- внешняя сторона сферы x2+y2+z2=a2.
Решение: Поверхностный интеграл ІІ рода сводим к трехкратному интегралу, используя формулу Гауса-Остроградського:
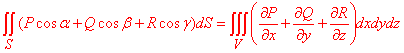
Выписываем P=P(x, y, z)=x3, Q=Q(x, y, z)=y3, R=R(x, y, z)=z3.
Тогда частичные производные от P, Q, R равны
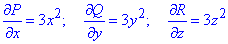
Область S ограничивает сфера V уравнением:
x2+y2+z2=a2.
В декартовой системе координат вычислять тройной интеграл когда объем ограничен сферой нецелесообразно, поскольку будем иметь корневые функции в пределах интеграла.
Поэтому всюду перейдем к сферической системе координат:
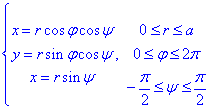
Находим частичные производные первого порядка по углам от параметризующих координат
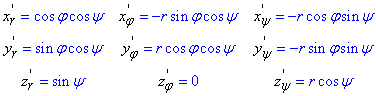
Дополнительно необходимо найти якобиан перехода:
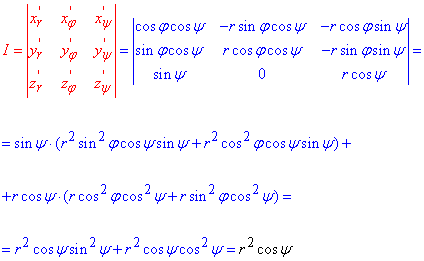
Он служит дополнительным множителем в интеграле.
Вычислим подынтегральное выражение в новых координатах:
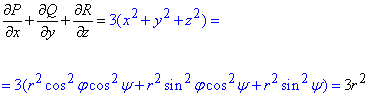
Дальше используя формулу Остроградського-Гауса находим поверхностный интеграл второго рода:
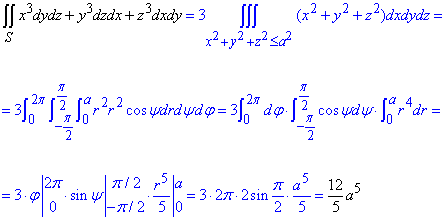
Внимательно пересмотрите как раскрывали внутренние интегралы в тройном.
Пример 5 Используя формулу Гаусса-Остроградського, превратить поверхностный интеграл
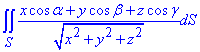
по гладкой поверхности S ограничивающей конечный объем V и 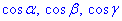 - направляющие косинусы внешней нормали к поверхности S.
- направляющие косинусы внешней нормали к поверхности S.
Решение: Имеем поверхностный интеграл ІІ рода
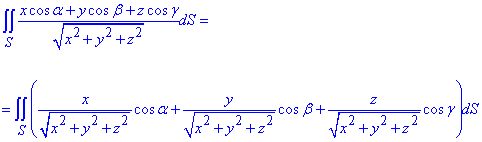
Сведем к объемному интегралу, используя формулу Гауса-Остроградського:
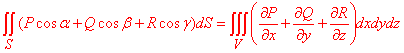
В соответствии с условием функции P, Q, R принимают значение
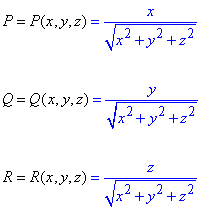
Вычисляем частичные производные второго порядка за переменными x, y, z
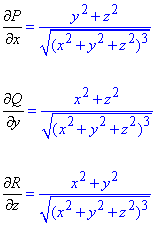
Подставляем и сводим интегрирование по площади на интегрирование по объему
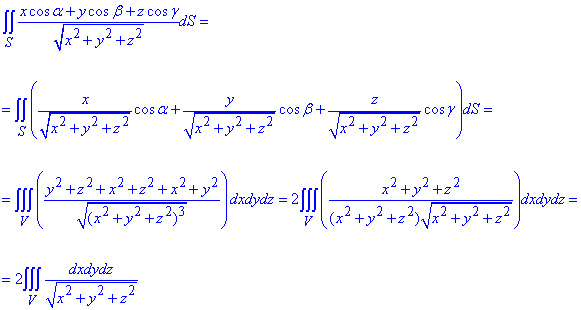
На сайте размещены сотни развязанных примеров из интегрирования, которые охватывают весь курс из интегралов.
Все что нужно для учебы Вы можете пересмотреть в категории интегрирования!


