Продовжуємо аналізувати відповіді до прикладів із ЗНО підготовки на ознаки подібності. Після паралельного перенесення та гомотетії точок йдуть приклади на паралельне перенесення прямих, парабол, кіл. Теорію з геометричних перетворень Ви можете знайти в онлайн доступі або почитати статтю "Геометричні перетворення. Перетворення подібності".
Далі розберемо розв'язки та формули на знаходження координат точок при повороті.
Тема: Перетворення фігур
Приклад 43.6 Дано точку C(1;3). Знайти координати точки C', у яку перейде точка C при повороті навколо початку координат на 900 проти годинникової стрілки.
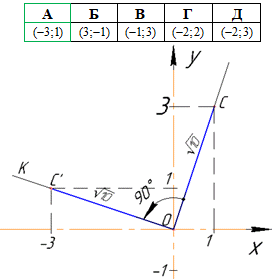
Розв'язування: Щоб побудувати точку C', у яку перейде точка C внаслідок повороту навколо точки O на кут α=90 градусів, потрібно (дивись рисунок):
а) провести промінь OC;
б) від променя OC відкласти кут COK, що дорівнює куту α у заданому напрямку (за умовою цього завдання – проти годинникової стрілки на кут α=90);
в) на промені OK знайти точку C', яка лежить на відстані OC від центру повороту O. Знайдемо довжини відрізка OC (і відповідно OC'):
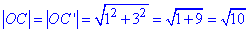
Якщо на промені OK від точки O відкласти відрізок |OC'|= √10, то отримаємо координати точки C'(-3;1).
Звичайно, що точно відкласти довжини більшості відрізків не зручно (або неможливо), тому для пошуку координат точки (x';y'), при попороті точки (x;y) на кут α проти годинникової стрілки, зручно використовувати формули:
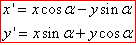
у нашому випадку, отримаємо
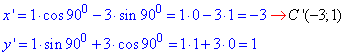
Відповідь: (-3;1) – А.
Приклад 43.17 Знайти образ точки (√2;0) при повороті навколо початку координат на кут 450 проти годинникової стрілки. 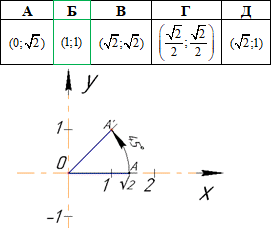
Розв'язування: Для пошуку координат образу точки (x';y'), при попороті точки (x;y) на кут α проти годинникової стрілки, зручно використовувати наступні формули:
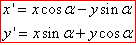
у нашому випадку точка A(√2;0) і кут α=45, отримаємо
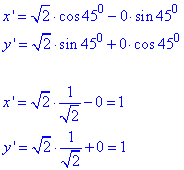
тобто A'(1;1).
У шкільних підручниках образи точок (фігур) при повороті рекомендують шукати через відкладання відповідних координат та відрізків (променів), але далеко не всі дійсні числа можна точно зобразити (наприклад, √2, 4/3 і т.д.), тому ми рекомендуємо використовувати вище наведені формули повороту для відшукання координат образу точок.
Відповідь: (1;1) – Б.
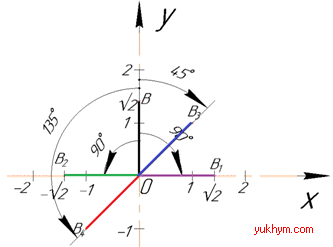
Приклад 43.22 Дано точку B(0;√2). Установити відповідність між поворотами навколо початку координат (1–4) та координатами образу точки (А–Д).
1. Поворот на 900 за годинниковою стрілкою | А. (1;1) |
Розв'язування: Для пошуку координат образу точки Bn(xn;yn), при попороті точки B(x;y) на кут α, зручно використовувати наступні формули:
- проти годинникової стрілки
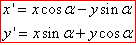 ,
,
- за годинниковою стрілкою
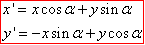
За наведеними залежностями визначаємо куди перейдуть точки з умови при повороті навколо O(0;0)
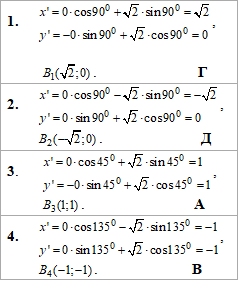
Тут мали наступні значення тригонометричних кутів:
sin(900)=0, cos(900)=0, sin(450)=cos(450)=sin(1350)=1/√2,
cos(1350)=-cos(450)=-1/√2.
Багато задач на геометричні перетворення можна розв'язати за допомогою наведених формул переходу точок при повороті. Зберігайте посилання на сайт та використовуйте в навчанні та ЗНО підготовці!


