В студентській практиці часто мало приводиться паралелей між прикладами, що вивчають на практичних та їх застосуванням до реальних задач, які чекають нас в житті.
Наведемо розрахунок купола на реальному прикладі.
Для наочності візьмемо церкву св. Димитрія в с. Мальчичі.
Ескіз креслень надали майстри.
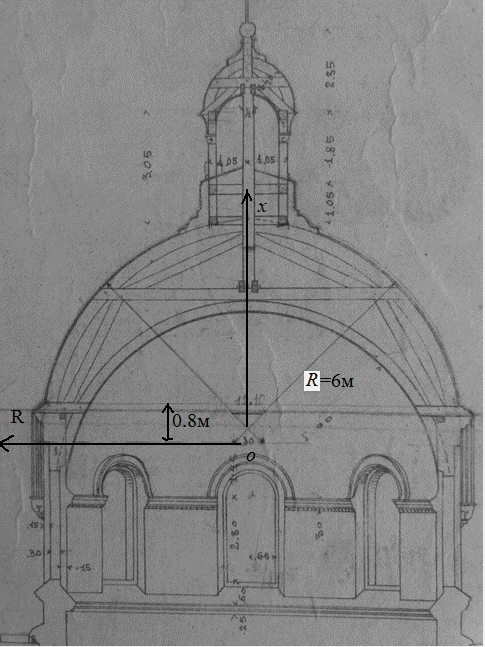
Потрібно знайти площу від основи над арками, і до верхньої циліндричної прибудови.
Зобразимо осі координат R перпендикулярно осі церкви, і вісь Ox – по осі церкви в напрямі вершини купола.
Слід зауважити, що наближені обчислення, коли форму модулюють півсферою з площею S=2Pi*R^2, дають велику похибку яку Ви оцінити не можете, тому що не знаєте правильного значення площі. Тому доцільно скористатися наведеною далі методикою.
Площу купола знаходимо через визначений інтеграл за формулою площі обертання кривої навколо осі
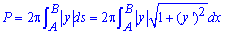
де ds - диференціал дуги кривої.
Обчислення виконаємо в математичному пакеті Maple17.
Крива що, обмежує купол має форму кола радіусом 6 м зміщеного на 30 см вбік, тому рівняння радіуса в залежності від біжучої координати х матиме вигляд
> R:=sqrt(6^2-x^2)-0.3;
![]()
Якщо форма купола відрізняється від кола то можна апроксимувати криву обертання поліномом четвертого R(x)=A*x^4+B*x^3+C*x^2+D*x+F чи вищого порядків методом найменших квадратів. Для цього знаходимо радіуси купола на різних висотах, а далі за вказаною вище методикою будуємо функцію R(x).
Для обчислення площ нас цікавить також радіус кола R1 на висоті 0.8 м та значення висоти (або координати х) коли купол дотикається до верхнього циліндра (надбудови) радіусом 1.05 м.
R1:=subs(x=0.8,R); R1:=5.646427499
> h:=solve(R=1.05,x);
h:=5.846152581
Нижню частину під куполом висотою 0.8 м можна розбити на циліндр висотою h1=0.65 м та зрізаний конус висотою h0=0.15 м.
Виступ цієї частини за знайдений радіус R1 приймаємо рівним 0.21 м.
Тому радіус в основі циліндра рівний R2=R1+0.21=5.85 м.
Побудова перерізу купола
змодельовані частини купола можемо зобразити графічно. Для цього в Maple підключаємо модуль plots та виконуємо побудову перерізів
> with(plots):
> q1:=plot(sqrt(6^2-x^2)-0.3,x=0..h,0..6,thickness=3):
q2:=plot(R2,x=0..0.65,thickness=3):
q3:=plot([[0.65,0], [0.65,R2], [0.8,R1], [0.8,0]],thickness=3):
q4:=plot([[h,0], [h,1.05]],thickness=3):
display(q1,q2,q3,q4);
в результаті отримаємо
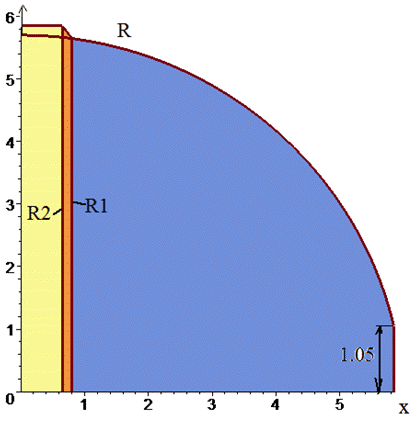
Знайдемо похідну від радіуса, що фігурує в формулі площі.
> DR:=diff(R, x);
![]()
Отримане значення підставляємо в підінтегральний вираз.
> F:=expand(R*sqrt(1+DR^2));
![]()
Тут виконано неповне спрощення формул, але це не суттєво, адже попереду ще потрібно знайти визначений інтеграл.
Повна площа поверхні купола
За допомогою функції інтегрування "int" знаходимо повну площу купола
> S[full_kupol]:=2*3.14*int(F,x=0..6);
Sfull_kupol:=208.324
Вона нас цікавить тільки для того, щоб кожен міг порівняти, який вплив дає зміщення осі на значення площі.
Знаходимо площу шуканої частини купола (замальовано синім на рисунку) через інтеграл від 0.8 м до висоти h де купол з'єднується з верхньою циліндричною частиною.
> S[kupol]:=2*3.14*int(F,x=0.8..h);
Skupol:=176.459
Площа циліндра під куполом
знаходимо за формулою S=2*Pi*R2*h1
> S[cylindr]:=2*3.14*R2*0.65;
Scylinder:=29.39040
Площа бічної поверхні зрізаного конуса
визначаємо через добуток твірної на суму радіусів основ і на число "Пі", оскільки маємо фігуру обертання
Skonus=Pi*l*(R1+R2)
де l – твірна конуса, R1, R2 – радіуси його основ.
Твірну конуса знаходимо з прямокутного трикутника:
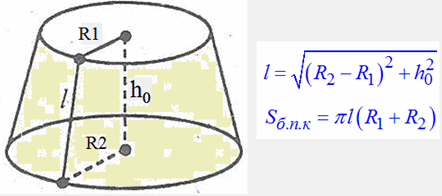
Різниця основ R2-R1 дасть нам один з катетів, інший рівний висоті h0=0.15 м.
За формулою Піфагора отримаємо
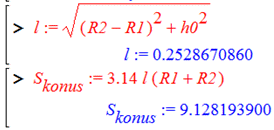
Сумарна площа купола + циліндра + зрізаного конуса
> SS:=S[kupol]+S[cylindr]+S[konus];
SS:=214.978 м2
Це і є відповіддь до поставленої на початку статті задачі.
Застосовуйте отримані формули на практиці.
Також маємо пропозицію до інженерів та майстрів, котрі виконують дерев'яну роботу на церквах чи покривають бляхою.
Якщо маєте проблеми при розрахунках з замовником, а саме – не знаєте як порахувати площу, звертайтесь до нас!
Ми можемо виконати розрахунок площі купола будь-якої складності.


