Продовжуємо аналізувати готові відповіді до тестових задач із ЗНО підготовки. Сьогодні Вашій увазі кілька поширених різнопланових прикладів на знання теорії про перпендикуляр та похилу в просторі. Пояснення не важкі і будуть зрозумілі як учням, так і їхнім батькам.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 35. Прямі та площини в просторі. Перпендикуляр та похила
Задача 35.12 Площини alpha і beta перетинаються по прямій a під кутом 600. Точка A належить площині alpha.
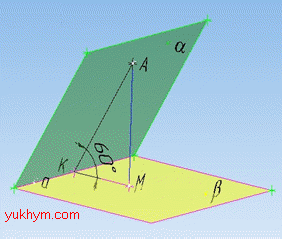
Довжина відрізка AM є відстанню від точки A до площини beta, а довжина відрізка AK – відстанню від точки A до прямої a. Знайти довжину відрізка AK, якщо AM=√3.
Розв'язання: Відстань від точки до площини – це перпендикуляр опущений з цієї точки на площину.
Основа перпендикуляра належить площині beta (в цій задачі це точка M), тому AM⊥beta.
Кут ∠AKM=60 – лінійний кут двогранного кута, тобто кут між площинами alpha і beta.
Розглянемо трикутник AMK. Оскільки AM⊥beta, то AM⊥MK (MK належить площині beta), тому ΔAMK – прямокутний (∠AMK=90), де AM=√3 – протилежний катет і ∠AKM=60.
За означенням синуса прямокутного трикутника знайдемо довжину відрізка (гіпотенузи) AK:
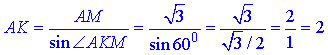
Відповідь: 2 – А.
Задача 35.13 Точка A віддалена від площини на відстань 6 √3 см.
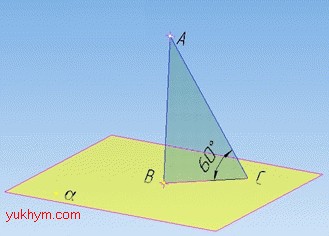
Обчислити довжину проекції похилої, проведеної з цієї точки під кутом 600 до площини.

Розв'язання: Відстань від точки до площини – це перпендикуляр опущений з цієї точки на площину.
Основа перпендикуляра належить площині alpha (в цій задачі це точка B), тому AB⊥alpha і AB=6 √3 см.
Нехай точка C (належить площині alpha) – основа похилої AC, а BC – проекція похилої на площину alpha. Звідси, ∠ACB=60.
Розглянемо трикутник ABC. Оскільки AB⊥alpha , то AB⊥BC (BC належить площині alpha), тому ΔABC – прямокутний (∠ABC=90), де AB=6 √3 см – протилежний катет і ∠ACB=60.
За означенням тангенса прямокутного трикутника знайдемо довжину відрізка (прилеглого катета до ∠ACB) BC:
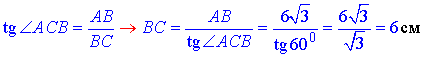
Відповідь: 6 см – Д.
Задача 35.16 На рисунку ABCD – квадрат, MB – перпендикуляр до площини ABC. Похила AM нахилена до площини ABC під кутом 450.
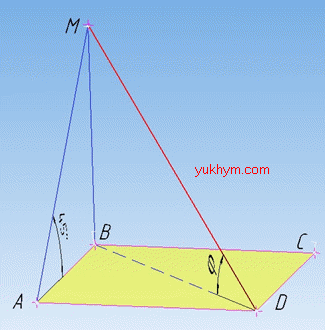
Під яким кутом нахилена до площини ABC похила MD?

Розв'язання: За умовою MB⊥(ABC), тому (за властивістю) вона перпендикулярна до кожної прямої, що належить площині ABC (квадрату ABCD), тобто MB⊥AB, MB⊥BC і MB⊥BD.
З умовою задачі маємо ABCD – квадрат, тому AB⊥BC.
Звідси випливає, що ∠MAB=45 – кут між похилою AM і площиною ABC, а ∠MDB – кут між похилою MD і площиною ABC (який і потрібно знайти), ∠MDB – ?
Позначимо через a довжину сторони квадрата ABCD, тобто AB=BC=CD=AD=a, тоді за теоремою Піфагора у прямокутному трикутнику ABD обчислимо діагональ квадрата ABCD:
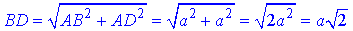
Розглянемо трикутник MAB. Оскільки MB⊥AB, то ΔMAB – прямокутний (∠MBA=90), де AB=a – катет і ∠MAB=45.
За теоремою про суму кутів трикутника:
∠AMB=180-90-45=45.
Звідси випливає, що ΔMAB – рівнобедрений за основою AM, тому AB=MB=a – бічні сторони ΔMAB.
Розглянемо трикутник MBD. Оскільки MB⊥BD, то ΔMBD – прямокутний (∠MBD=90), де MB=a – протилежний катет до ∠MDB і BD=a√2 – прилеглий катет.
За означенням тангенса прямокутного трикутника знайдемо ∠MBD:
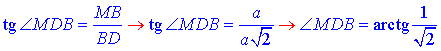
Відповідь: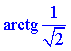 – Г.
– Г.
Задача 35.17 З вершини A квадрата ABCD до його площини проведено перпендикуляр AK завдовжки 6 см.
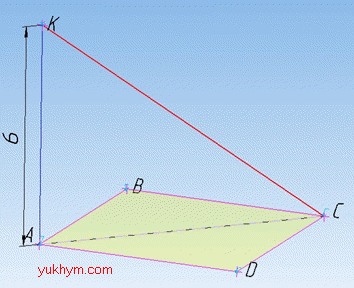
Знайти відстань від точки K до вершини C квадрата, якщо його сторона дорівнює 4√2 см.
Розв'язання: За умовою AK⊥(ABC), тому (за властивістю) вона перпендикулярна до кожної прямої, що належить площині ABC (квадрату ABCD), тобто AK⊥AC, де AC – діагональ квадрата ABCD, проекція похилої KC на площину ABC.
Розглянемо квадрат ABCD. За умовою AB=BC=CD=AD=4√2 см.
Знайдемо діагональ AC. За теоремою Піфагора у прямокутному трикутнику ΔABC (∠ABC=90) маємо:
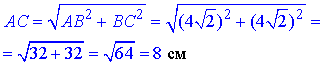
Розглянемо трикутник AKC. Оскільки AK⊥AC, то ΔAKC – прямокутний (∠KAC=90), де AK=6 см – катет і AC=8 см – катет.
За теоремою Піфагора знайдемо довжину відрізка, гіпотенузи KC (відстань від точки K до вершини C квадрата ABCD):
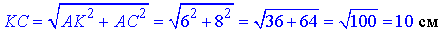
Відповідь: 10 см – Д.
Ще кілька готових завдань на перпендикуляр та похилу в просторі чекають на Вас у наступній статті.



