підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 53. Знайдіть проміжки зростання і спадання та точки екстремуму функції:
1) 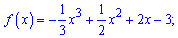
Розв'язання: ОДЗ полінома вся дійсна вісь 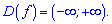
Обчислюємо похідну
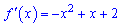
та прирівнюємо до нуля
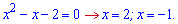
Між коренями похідна додатна
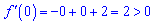
значить функція зростає на проміжку 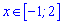 та спадає на сусідніх
та спадає на сусідніх 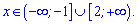
В -1 маємо мінімум, а в 2 функція досягає максимуму. Значення ординати в точках екстремуму наступні
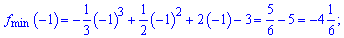
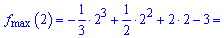
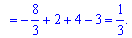
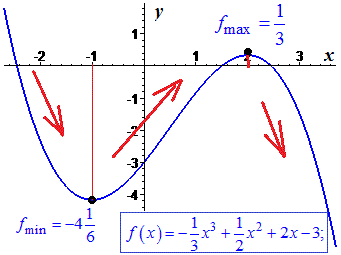
Графічно знайдені точки екстремуму та проміжки монотонності наведено на рисунку
2) f(x)=x4-2x2+3
Розв'язання: ОДЗ біквадратної функції дійсна вісь 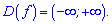
З рівності похідної нуля визначаємо критичні точки
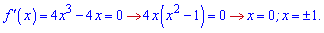
Отримали 3 точки, встановлюємо знак похідної на інтервалах
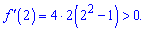
Маємо два проміжки зростання функції
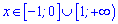
та два де функція спадає
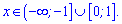
В одиниці та мінус одиниці маємо мінімуми і максимум в нулі.
Значення функції в точках екстремуму наступні
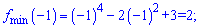
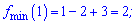
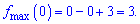
Графік полінома із знайденими екстремумами наочно ілюструє пророблену роботу
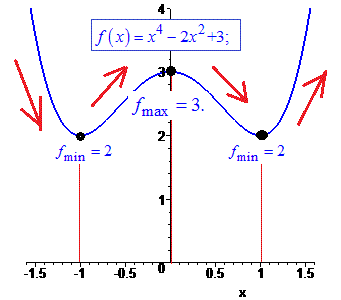
3) 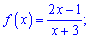
Розв'язання: ОДЗ дробової функції всі точки за винятком (-3 – нуль знаменника). 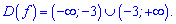
Обчислюємо похідну від частки
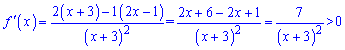
Похідна додатна на всій області визначення, а отже функція всюди зростає.
Її графік має вигляд
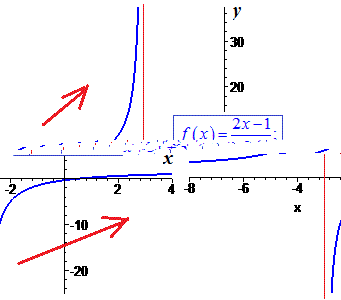
4) 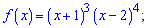
Розв'язання:ОДЗ функції множина дійсних чисел 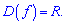
З рівності нулю похідної встановимо критичні точки
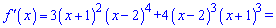
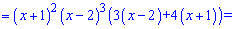
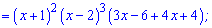
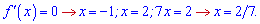
Числову вісь розбиваємо знайденими точками на інтервали та встановлюємо знаки похідної 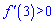 .
.
Оскільки дужки 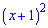 є в парному степені, то при переході через (-1) похідна не змінює знак.
є в парному степені, то при переході через (-1) похідна не змінює знак.
Функція зростає на 3 інтервалах
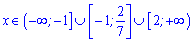
та спадає на проміжку
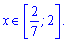
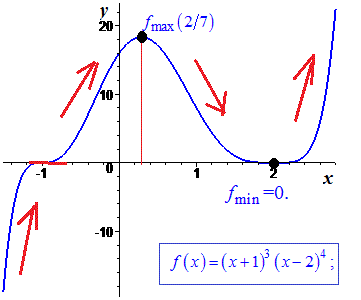
Отримали точку мінімуму x=2, точку максимуму x=2/7 та перегину x=-1.
Ордината точки мінімуму
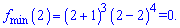
Максимум 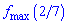 спробуйте обчислити самостійно, надто дробове число має вийти.
спробуйте обчислити самостійно, надто дробове число має вийти.
Наглядний графік функції дає ясність на багато речей
5) 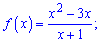
Розв'язання: ОДЗ функції вся вісь крім нуля знаменника
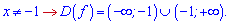
Шукаємо похідну від частки
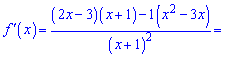
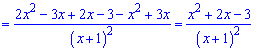
та критичні точки функції
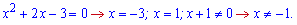
При переході через (-1) похідна не змінює знак, так як знаменнику дужка в парному степені. В нулі похідна менша нуля
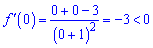
отже на інтервалі між (-1) і 1функція спадає. Далі розставляємо знаки похідної згідно правил
Отримали, що функція зростає на інтервалах
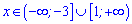
та спадає посередині 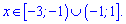
При x=-3 маємо максимум, в точці x=1 – мінімум функції.
Ординати екстремумів обчислюємо підстановкою в функцію
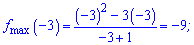
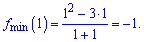
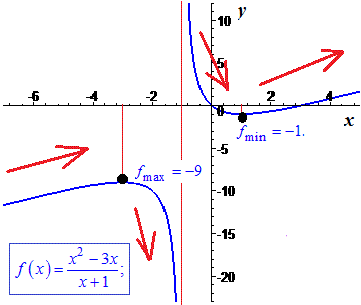
Особливості поведінки відображає графік функції
6) 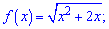
Розв'язання: Область визначення встановлюємо з умови обмеження кореня
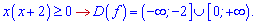
Обчислюємо похідну
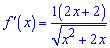
і знаходимо критичні точки
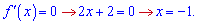
Дана точка не належить області визначення До них добавляємо нулі знаменника
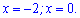
Перевіряємо знак похідної в одиниці
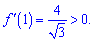
Отже функція зростає на інтервалі
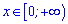
та спадає при
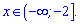
Точок екстремуму функція немає, а її графік має вигляд
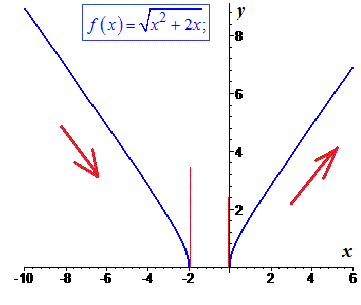
7) 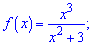
Розв'язання: Область визначення вся вісь, оскільки знаменник завжди більший нуля.
Визначимо критичні точки функції
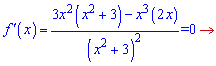
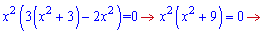
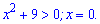
Крім того точка x=0 є точкою перегину, оскільки змінна входить в похідну при парному степені. Похідна всюди додатна, отже функція зростає на множині дійсних чисел і немає точок екстремуму.
Графік функції наведено нижче
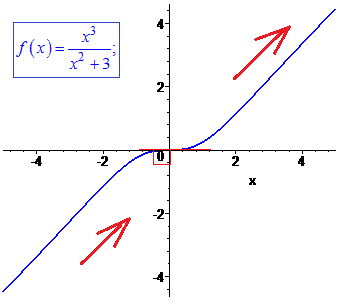
8) 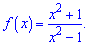
Розв'язання: Область визначення обмежена двома нулями знаменника
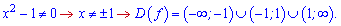
Встановимо критичні точки функції
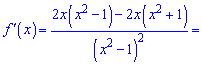
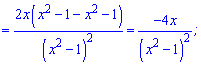
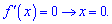
Функція спадає при більших значеннях змінної за нуль
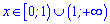
та зростає зліва від інтервалів
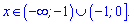
В нулі маємо максимум
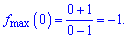
Графік функції із встановленими характеристиками наступний
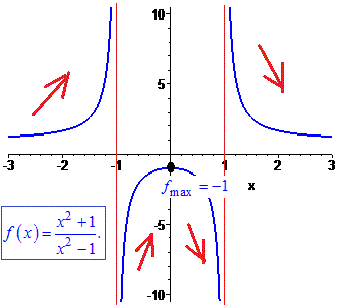
Приклад 54. Знайдіть, при яких значеннях a функція
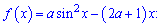
1) не має критичних точок;
2) не має точок екстремуму.
Розв'язання:
1) Область визначення вся дійсна вісь.
Не має критичних точок означає, що похідна не дорівнює нулеві.
Знайдемо похідну
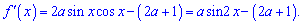
Визначимо параметр a
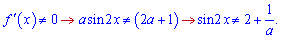
Синус приймає значення від (-1) до 1. Необхідно, щоб права сторона приймала значення за межами проміжку
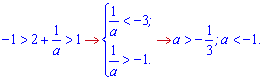
Отримали два інтервали розв'язків
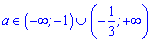
2) На краях знайденого інтервалу критичні точки будуть перегинами, це слідує з вигляду функції перша –періодична парна, друга – рівняння прямої. Тобто на краях немає точок екстремуму
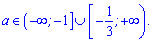
Переконатися в цьому Ви можете з графіків відповідних функцій
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Точки екстремуму функції. №52
- Наступні відповіді - Найбільше і найменше значення функції на відрізку
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



