підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 52. Знайдіть точки екстремуму функції:
1) 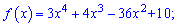
Розв'язання: Областю визначення полінома є вся дійсна вісь 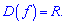
Знаходимо похідну функції
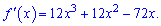
Прирівнюємо її до нуля, попередньо винісши за дужки змінну, та визначаємо підозрілі на екстремум точки
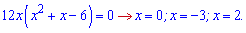
Отримали три критичні точки. Перевіряємо знак похідної між ними, щоб з'ясувати яка з них буде точкою мінімуму, а яка – максимуму.
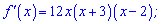
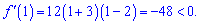
На інтервалі (0;2) похідна від'ємна, в сусідніх інтервалах знаки похідної чергуються.
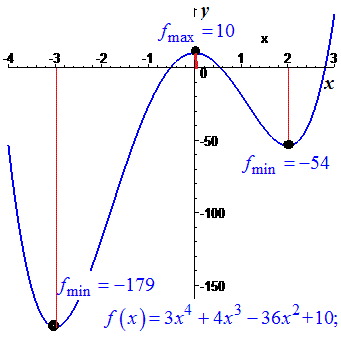
Отримали 2 точки мінімуму x=-3;x=2 та одну максимуму x=0.
Знайдемо значення функції в точках екстремуму
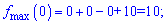
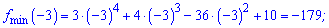
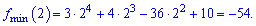
Отже, (0;10) – точка максимуму;
(-3;-179), (2;-54) – точки мінімуму.
На графіку функції точки екстремуму матимуть вигляд
2) 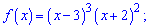
Розв'язання:
ОДЗ – множина дійсних чисел 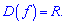
Похідну від добутку функцій прийме вигляд

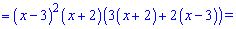
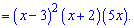
З умови рівності нулю похідної отримаємо три критичні точки
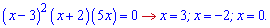
Перевіряємо знак похідної в одиниці
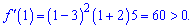
Отже після нуля функція зростає, а значить x=0 є точкою мінімуму, відповідно x=-2; x=3 – точками підозрілими на максимум. Точку x=3 потрібно відкинути, оскільки з вигляду похідної бачимо, що наступна похідна в цій точці перетворюється в нуль. Отже x=3 – точка перегину. Обчислюємо екстремуми функції
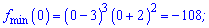
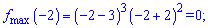
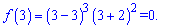
Отримали максимум (-2;0) та мінімум функції (0;-108). На графіку знайдені екстремуми зображені точками
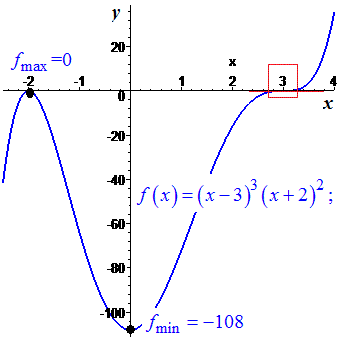
3) 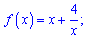
Розв'язання:
ОДЗ – множина дійсних чисел за винятком нуля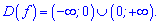
Обчислюємо похідну
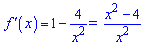
та прирівнюємо її до нуля
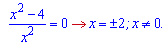
Наносимо критичні точки на числову вісь. Знак похідної перевіряємо підстановкою точки з інтервалу, наприклад одиниці
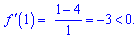
Похідна менша нуля, отже функція спадає. При переході через нуль знак не змінюється, оскільки знаменник похідної в парному степені, а далі чергується "-" з "+".
Отримали максимум в точці x=-2 та мінімум x=2.
Обчислимо ординати точок екстремуму
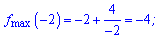
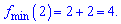
Не лякайтесь, що значення функції в максимумі менше за відповідне в мінімумі. Це всього навсього локальні екстремуми і така ситуація нормальна.
Графік функції з наведеними точками зображено нижче
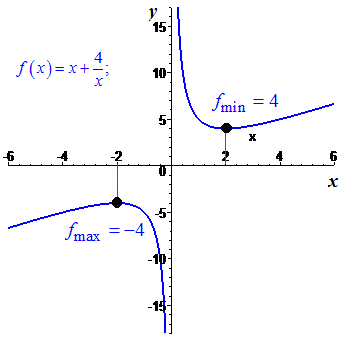
4) 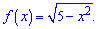
Розв'язання:
ОДЗ отримаємо з обмеження на кореневу функцію
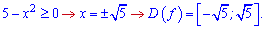
Обчислюємо похідну функції
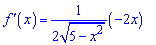
та визначаємо критичну точку
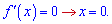
Справа похідна від'ємна
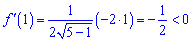
значить функція спадає, я точка x=0 є максимумом.
Максимум функції рівний
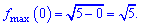
Графіком функції є півколо
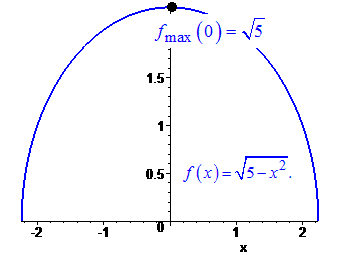
Ось такий порядок відшукання точок екстремуму Ви повинні вивчити та застосовувати на практичних заняттях, тестах, контрольних.
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Точки екстремуму функції
- Наступні відповіді - Точки екстремуму функції. №53-54
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



