підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 55. Знайдіть найбільше і найменше значення функції на даному проміжку:
1) 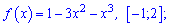
Розв'язання: Функція досягає свого найбільшого (найменшого) значення або в критичних точках, або на краях проміжку. Встановимо критичні точки функції, для цього обчислюємо похідну
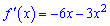
і прирівнюємо її до нуля
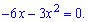
Розклавши на прості множники,
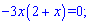
отримаємо два корені
x=0; x=-2
один з яких не належить розглядуваному проміжку
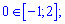

Обчислюємо значення функції в критичній точці та на краях області
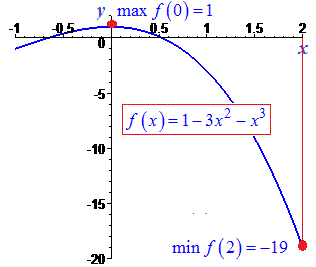
f(0)=1; f(-1)=1-3+1=-1; f(2)=1-12-8=-19.
Отримали максимум функції в критичній точці
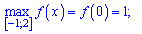
та мінімум на краю
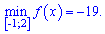
Графік функції в заданому проміжку наведено на рисунку
2) 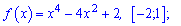
Розв'язання: Обчислюємо похідну функції
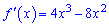
та прирівнюємо її до нуля.
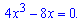
Встановлюємо корені рівняння
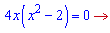
x=0;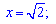
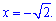
Дві критичні точки належать розглядуваному проміжку
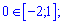
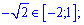
одна знаходиться за його межами
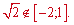
Обчислюємо значення функції в усіх підозрілих точках
f(0)=2; 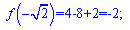
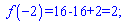
f(1)=1-4+2=-1.
Отримали, що максимум досягається одночасно в двох точках
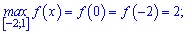
а мінімум в третій
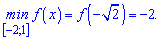
Графік функції наведено нижче
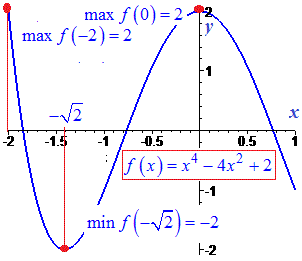
3) 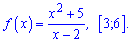
Розв'язання: За наведеною схемою спочатку обчислюємо похідну функції.
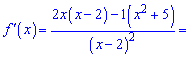
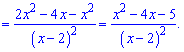
З умови рівності нулю похідної або її не існування визначаємо критичні точки
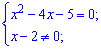
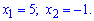
Одну з них беремо до розгляду, інша випадає
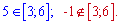
Послідовно знаходимо значення функції
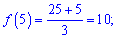
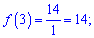
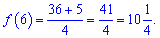
Порівнянням значень, визначаємо максимум та мінімум функції на проміжку.
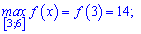
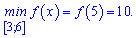
Функція на проміжку зображена графічно
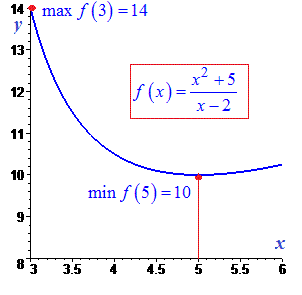
4) 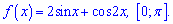
Розв'язання: Записуємо умову рівності нулю похідної
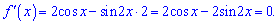
З неї розписуємо рівняння та знаходимо критичні точки
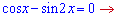
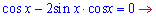
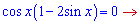
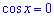 або
або 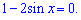
З першого рівняння розв'язок буде наступним
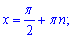
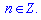
Друге рівняння розписуємо
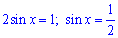
та знаходимо корені
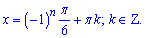
Три з них 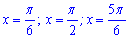 - належать проміжку.
- належать проміжку.
Знаходимо значення функції в критичних точках
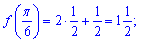
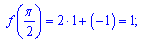
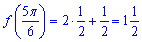
та на краях проміжку
f(0)=1; f(Pi)=0+1=1.
Отримали дві точки, де функція досягає максимуму
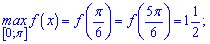
та три точки мінімуму функції
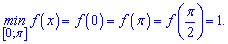
Фрагмент графіку наведено нижче 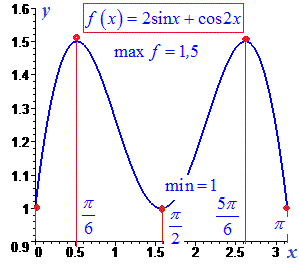
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Точки екстремуму функції. №53-54
- Наступні відповіді - Найбільше і найменше значення функції на відрізку. №56-61
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



