ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 98. Розв'яжіть систему рівнянь:
1) 
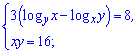
Розв'язання:
Починаємо аналіз з окреслення області визначення. За властивістю логарифма маємо
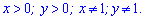
Перепишемо перше рівняння системи у вигляді
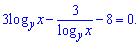
Позначимо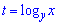 
, та при умові, що вираз відмінний від нуля, зводимо рівняння до квадратного множенням на знаменник
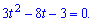
Обчислюємо дискримінант квадратного рівняння
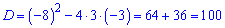
та корені
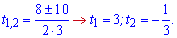
Повертаємося до заміни, яку робили вище і знаходимо невідому x
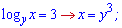
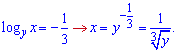
Щоб остаточно визначити змінні використаємо друге співвідношення із системи рівнянь
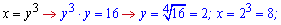
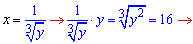
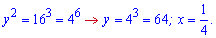
В результаті нескладних перетворень отримали дві пари розв'язків системи логарифмічних рівнянь
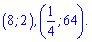
Обчислення даного завдання завершено.
2) 
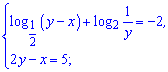
Розв'язання:
Починаємо із зведення другого доданку до однієї основи. Для цього використаємо дві властивості логарифма, їх детально я Вам випишу, а на практиці пам'ятайте про них
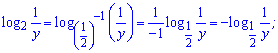
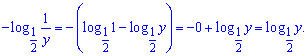
Ось так просто отримали потрібний вигляд. Підставляємо в систему
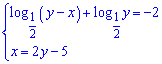
Тут в другому рівнянні виразили одну змінну через іншу. Далі за наведеною вище схемою встановлюємо ОДЗ
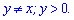
Підставляємо змінну в перше рівняння і розв'язуємо його
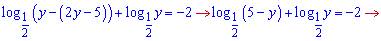
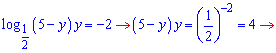
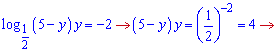
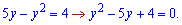
За теоремою Вієта коренями квадратного рівняння будуть y=1;y=4.
Підставляємо в друге рівняння системи та обчислюємо розв'язок
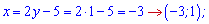
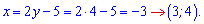
Знову отримали два розв'язки.
3) 
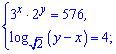
Розв'язання:
Такого роду приклади розв'язують за інакшою схемою ніж попередні. З логарифмічного рівняння отримують залежність між змінними, далі виражають одну змінну через іншу та підставляють в показникове рівняння. Воно як правило не складне і використовуючи властивості показників встановлюють розв'язки. Перейдемо до реалізації на практиці даного методу.
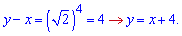
Підставимо в показникові рівняння
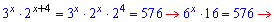
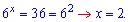
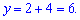
Розв'язок системи рівнянь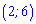 
також задовольняє ОДЗ 
.
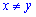Досить швидко можна отримати розв'язки усіх подібних завдань, головне дотримуватися наведених схем.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Логарифмічні нерівності. №96, 97
- Наступні відповіді - Системи показникових і логарифмічних рівнянь. №98
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
