підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 96. Розв'яжіть нерівність:
1)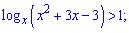
Розв'язання. Це просто "мегазадача" на логарифмічні нерівності – в основі міститься змінна: залежно чи основа більша, чи менша одиниці отримаємо нерівності з протилежним знаком. Зайві розв'язки потрібно відсікти, а потімі для обох нерівностей об'єднати. Одним словом – "дивіться і вчіться"!
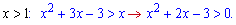
За теоремою Вієта x=-3; x=1. В нулі квадратична нерівність від'ємна, тобто не виконується. З врахуванням того, що розглядаємо розв'язки при x>1 отримаємо один інтервал
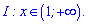
Тепер, нехай основа менша одиниці
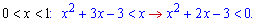
Це виконується між знайденими вище коренями 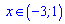 .
.
Проміжок, на якому розв'язуємо вносить наступні зміни в знайдений інтервал
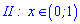 .
.
Все би було добре, якби не одне але: де Ви тут бачили перевірку ОДЗ?
Її немає! Ніколи не забувайте перевіряти ОДЗ, вона в більшості випадків вносить свої поправки в кінцевий результат.
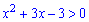
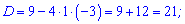
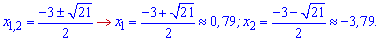
Приблизні значення наведені для того, щоб легше було зорієнтуватися де вони розміщені на числовій осі.
Підстановкою нуля бачимо, що нерівність виконується за межами інтервалу між коренями, тобто ОДЗ складається з наступних інтервалів

Остаточно встановлюємо, що ОДЗ звузила другий інтервал, а нерівність має наступний розв'язок
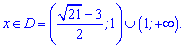
2) 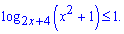
Розв'язання. Завдання теж не з простих. Того разу почнемо аналіз з області визначення:
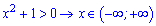
виконується при будь-яких змінних x.
А) Розв'язуємо при основі більшій за одиницю
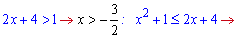
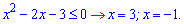
В нулі нерівність виконується. Разом з умовою на проміжок x>-1,5 отримаємо інтервал
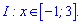
Б) Основа менша одиниці:
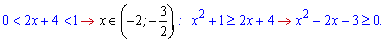
Рівняння те саме, тільки помінявся знак в нерівності. Відповідно тепер інтервал між коренями не є розв'язком, а за його межами нерівність виконується. Додаємо до цього умову на проміжок і отримаємо
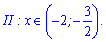
Оскільки ОДЗ не накладає жодних обмежень, то обидва інтервали будуть розв'язками логарифмічної нерівності
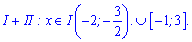
Приклад 97. При яких значеннях а число -1 є розв'язком нерівності
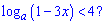
Розв'язання. Не варто виписувати складних рівнянь.
У завданні вже міститься підказка частина розв'язку: підставляємо (-1) в нерівність і розв'язуємо відносно параметра a.
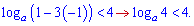
Розглядаємо можливі варіанти:
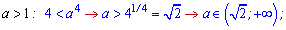
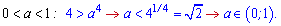
В останньому рядку вийшла одиниця через умову a<1. Виписуємо перетин розв'язків як кінцеву відповідь
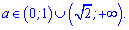
На цьому приклади вичерпалися і переходимо до нової теми.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Логарифмічні нерівності. №95
- Наступні відповіді - Системи показникових і логарифмічних рівнянь
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



