ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 18. Знайдіть похідну функції:
1)
Похідна від частки двох функцій обчислюється за правилом
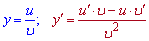
Формулу похідної від частки функцій застосовуємо до цього та всіх наступних прикладів.
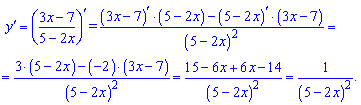
2) 
Знаходження похідної від дробової функції не важке, якщо в чисельнику і знаменнику маємо поліноми.
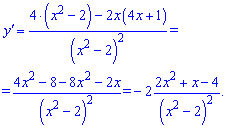
3) 
Похідна від частки рівна дробовій функції
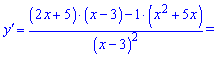
4) 
Обчислюємо похідну дробової функції
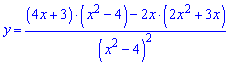
Після множення доданків чисельника і групування подібних Ви отримаєте
5)
Похідна функції прийме вигляд
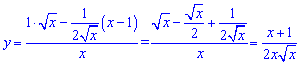
6) 
Знаходимо похідну дробової функції
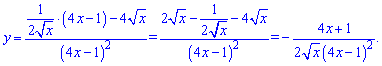
7)
У завданні головне знати похідну від синуса
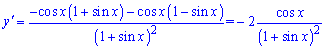
все решта – це спрощення.
8)
Застосовуємо похідну частки
Приклад 19. Обчисліть значення похідної даної функції при вказаному значенні незалежної змінної:
1) 
Знаходимо похідну частки функцій
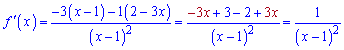
Підставляємо задану точку
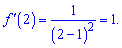
2) 
Похідна набуде вигляду
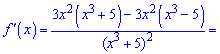
Знаходимо похідну в точці
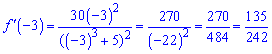
Останній дріб можна спростити діленням в стовпчик або на калькуляторі (0,55785).
Приклад 20. Чи є правильним твердження, що похідна першої функції в одиниці менша похідної від другої 
де функції приймають значення
Розв'язання:
Обчислюємо похідні від обох функцій
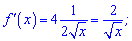
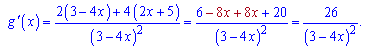
Знаходимо значення похідних в одиниці
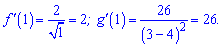
Маємо виконання нерівності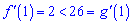 
, тобто
твердження справедливе.
Приклад 21. Розв'яжіть нерівність похідних 
якщо функції мають вигляд
Розв'язання:
Знаходимо похідні
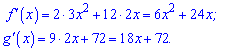
Підставимо в нерівність
За теоремою Вієта знаходимо корені квадратного рівняння
Перевіримо знак функції. Для цього підставимо будь-яку точку, для зручності х=0
Отже між коренями функція приймає від'ємні значення.
Оскільки нерівність нестрога, то краї проміжку входять в розв'язок.
Приклад 22. Знайдіть, при яких значеннях х похідна функції рівна нулю
Розв'язання:
Похідна функції наступна
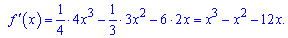
Прирівнюємо до нуля і розв'язуємо
Перший розв'язок х=0, інші два за теоремою Вієта приймають значення х=4 та х=-3.
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Правила обчислення похідних. № 15-17
- Наступні відповіді - Похідна складеної функції
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал -порекомендуйте друзям!
