підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 25. Знайдіть похідну функції:
Правила знаходження похідних для складених тригонометричних функцій такі ж як і для показникових
1) y=cos(6x)
Обчислюємо похідну від косинуса
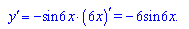
2) 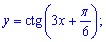
Похідна від котангенса прийме значення
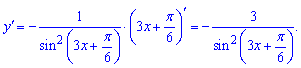
3) 
Обчислюємо похідну синуса в квадраті за правилом складеної функції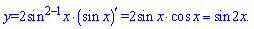
4) 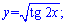
На цьому прикладі правило застосовуємо двічі: до підкореневої функції та аргументу тангенса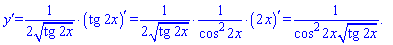
5) 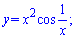
Похідна від добутку функцій буде наступною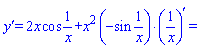
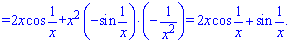
6) 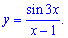
Похідна від дробової функції обчислюється за простою формулою, тут ише не забуваємо, що sin(3x) складена функція
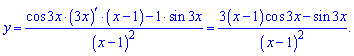
Приклад 26. Обчисліть значення похідної даної функції в точці х0:
1) 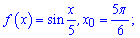
Похідна від синуса рівна
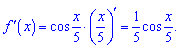
Підставляємо значення кута в знайдену формулу
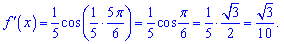
2) 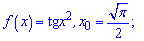
Похідна від квадрату тагенса рівна
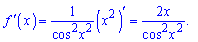
Обчислюємо значення похідної в заданій точці
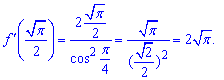
3) 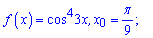
Тут правило для похідної складеної функції застосовуємо двічі. Завжди слідкуйте за виглядом функцій
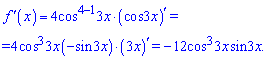
Знаходимо значення похідної в точці
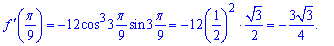
4) 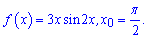
Похідна від добутку функцій
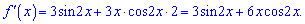
в точці (Pi/2) рівна -3Pi.
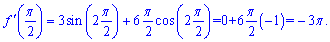
Приклад 27. Розв'яжіть рівняння f'(x)=g(x) якщо функції приймають значення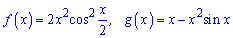
Розв'язання:
Обчислюємо похідну першої функції
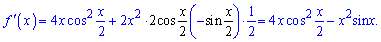
Складаємо рівняння
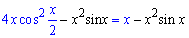
та розв'язуємо його відносно змінної
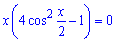
Один корінь рівняння рівний нулю.
Інший знаходимо з тригонометричного рівняння
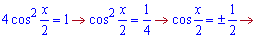
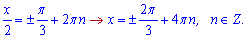
Отримали три розв'язки рівняння
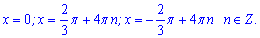
Приклад 28. При яких значеннях х похідна функції
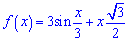
більша за нуль?
Розв'язання:
Знаходимо похідну наведеної функції
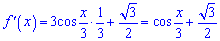
Прирівнюємо отриману залежність до нуля і розв'язуємо нерівність
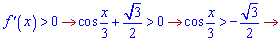
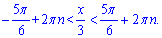
Домножимо на три і отримаємо шуканий розв'язок
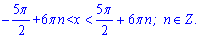
Уважно перегляньте приклади застосування похідної складеної функції. Завдання достатньо прості та наочно показують силу усіх правил.
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Похідна складеної функції
- Наступні відповіді - Дотична до графіка функції
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал -порекомендуйте друзям!



