ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 110. Знайдіть проміжки зростання і спадання та точки екстремуму функції:
13) 
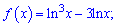
Розв'язання.
Область визначення – додатна вісь. Знаходимо похідну логарифмів
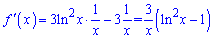
та прирівнюємо до нуля
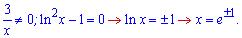
Підставимо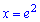 
у похідну
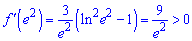
Отже експонента буде точкою мінімуму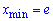 
, а попередня точка 
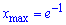– максимумом. Зростає функція на двох інтервалах
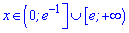
і спадає на проміжку
.
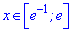14) 
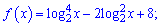
Розв'язання.
Область визначення – x>0. Обчислюємо похідну
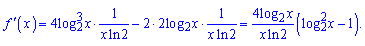
Шукаємо критичні точки
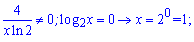
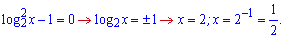
Розбиваємо додатну вісь на інтервали і встановлюємо знак похідної. Для зручності, оскільки логарифм двійковий можете вибрати 4. Не важко переконатися, що похідна більша за нуль
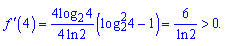
На попередніх інтервалах знаки змінюються. Таким чином маємо дві точки мінімуму
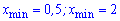
та одну максимуму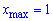 
Інтервали зростання функції наступні
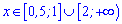
Інтервали спадання функції –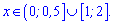 
15) 
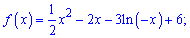
Розв'язання.
За рахунок знаку "-" областю визначення буде від'ємна вісь. Це перший такий приклад. Знаходимо похідну,
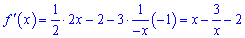
а далі за відомою вже схемою
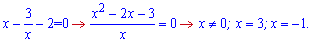
x=3 не враховуємо – нас цікавить тільки від'ємна вісь. Розбиваємо на інтервали і підстановкою x=-3 встановлюємо знак похідної
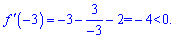
Похідна від'ємна, отже знайдено точку мінімуму
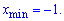
Функція зростає при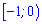 
, спадає лівіше від цього інтервалу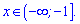 
16) 
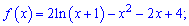
Розв'язання.
Встановлюємо ОДЗ
Дальше за планом визначаємо похідну та точки екстремуму
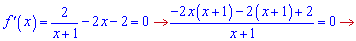
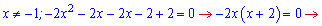
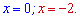
Другий корінь не належить ОДЗ. В одиниці похідна від'ємна,
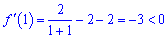
отже функція спадає в даному інтервалі, а знайдена точка є максимумом
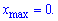
Функція зростає на (-1;0], та спадає на продовженні
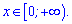
17) 
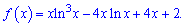
Розв'язання.
Область визначення – x>0. Похідна рівна нулю
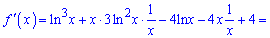
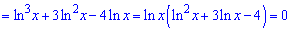
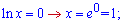
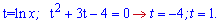
Повертаємося до заміни
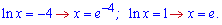
Підставимо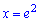 
в похідну, щоб перевірити знак
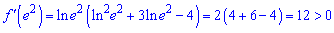
Будуємо графік знакосталості функції
Функція зростає на
,
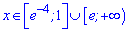спадає на інтервалах
-------------------------------------------------------------
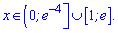
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Похідна показникової та логарифмічної функцій. №110 (8-12)
- Наступні відповіді - Похідна показникової та логарифмічної функцій. №111
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
