підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 111. Знайдіть найбільше і найменше значення функції f(x) на даному проміжку:
1) 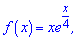 [-8;0];
[-8;0];
Розв'язання.
Функція досягає свого максимуму (мінімуму) або в критичних точках, або на краях проміжку. Цим і користуємося при обчисленні. Знаходимо похідну
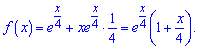
Прирівнюємо її до нуля
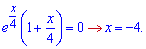
Точка належить досліджуваному проміжку. Обчислюємо значення функції в точках
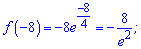
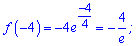
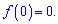
Порівнюючи значення отримаємо максимуми і мінімуми на відрізку
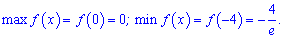
2) 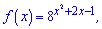 [-2;0];
[-2;0];
Розв'язання.
Похідна функції 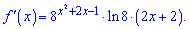
Перші два множники завжди більші нуля. Звідси маємо
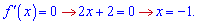
Точка міститься в розглядуваній області. Обрахуємо значення функції
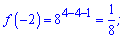
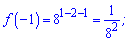
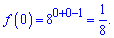
На краях функція приймає максимальні значення,
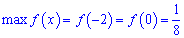
а в знайденій точці має мінімум
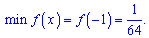
3) 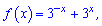 [-1;2];
[-1;2];
Розв'язання.
Похідна показникової функції
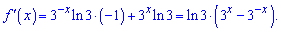
Знаходимо точку екстремуму
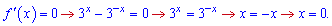
Вона належить проміжку
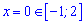
Обчислюємо значення функції на краях проміжку та в знайденій точці
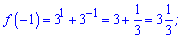
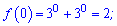
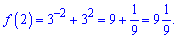
Останнє значення буде максимумом на проміжку,
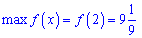
а в критичній точці мінімум
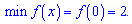
4) 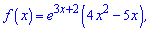 [0;2];
[0;2];
Розв'язання.
Похідна від добутку прийме значення
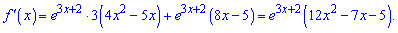
З умови на екстремум отримаємо квадратне рівняння
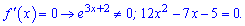
яке розв'язуємо через дискримінант
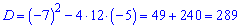
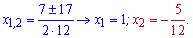
Перший корінь належить проміжку, другий – ні. Обчислюємо значення функції
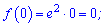
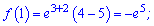
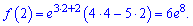
Максимум буде в точці
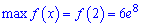 ,
,
мінімум
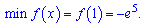
5) 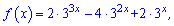 [-1;1].
[-1;1].
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Похідна показникової та логарифмічної функцій. №110 (13-17)
- Наступні відповіді - Похідна показникової та логарифмічної функцій. №112 (1-4)
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



