ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 113. При яких значеннях а функція
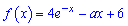
не має критичних точок?
Розв'язання.
Щоб функція не мала критичних точок необхідно, щоб її похідна не перетворювалася в нуль.
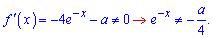
Показникова функція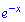 
завжди додатна, отже права сторона має бути від'ємною
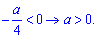
Отже при всіх додатних значеннях параметра а функція не має критичних точок.
---====================---
Приклад 114. При яких значеннях а функція
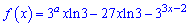
спадає на множині дійсних чисел?
Розв'язання.
Спадною функція буде при від'ємній похідній. Обчислюємо похідну
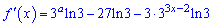
та підставляємо в умову
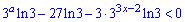
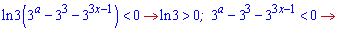
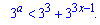
Оскільки показникові функція на множині дійсних чисел більша нуля
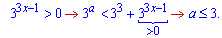
то параметр а не повинен бути більший за трійку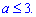 
---====================---
Приклад 115. Знайдіть проміжки зростання і спадання функції
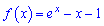
і доведіть, що умова
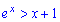
виконується при х > 0 .
Розв'язання.
Знаходимо похідну функції
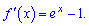
Визначимо критичну точку
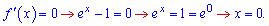
При більших значеннях за 0 похідна додатна, отже функція зростає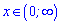
, а при менших спадає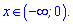 
Доведення нерівності виконаємо на основі наступних міркувань. Перепишемо її у вигляді функції
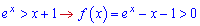
Функція рівна нулю в точці x=0. Вище через похідну було встановлено, що функція зростає при додатних значеннях аргументу (x>0), тобто з ростом аргументу значення функції буде більше ніж в нулі. Таким чином нерівність доведена.
---====================---
Приклад 116. Знайдіть проміжки зростання і спадання функції
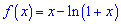
і доведіть, що нерівність
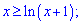
виконується при х>-1.
Розв'язання.
Завдання аналогічне попередньому. Обчислюємо похідну
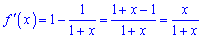
та визначаємо критичні точки
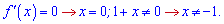
Остатня умова також випливає з області визначення логарифма
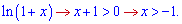
При більших значеннях за нуль функція зростає
,
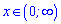при менших – спадає
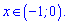
Доведення нерівності досить просте. Точка нуль є точкою мінімуму, крім того в нулі функція рівна нулю
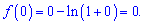
Тобто справа
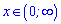
і зліва від нуля
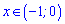
нерівність виконується строго
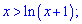
і лише в нулі маємо рівність
.
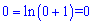Якщо ці два інтервали об'єднати то отримаємо, що нерівність має місце при значеннях х>-1.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Похідна показникової та логарифмічної функцій. №112 (5-8)
- Наступні відповіді - Перестановки
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
