підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 100. Обчисліть значення похідної даної функції в точці x0:
1) 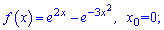
Обчислюємо похідну функції
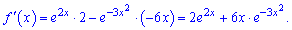
Підставляємо замість змінної значення в точці
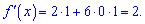
На цьому всі обчислення, переходимо до наступного завдання.
2) 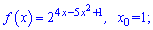
Знаходимо похідну показникової функції
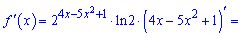
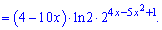
Підставимо задану точку x0:
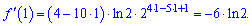
Завдання виконано.
3) 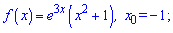
Знаходимо похідну від добутку
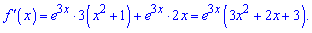
Підставляємо в похідну значення точки
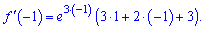
Спрощення в дужках виконайте самостійно.
4) 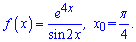
Приклад 101. Розв'яжіть нерівність похідних 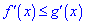 , якщо функції приймають значення:
, якщо функції приймають значення:
1)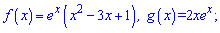
Розв'язання.
Обчислимо похідні від двох функцій
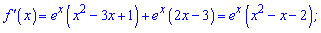
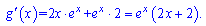
Записуємо похідні в нерівність
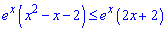
Оскільки експонента завжди більша нуля, то на неї можемо поділити і перейти до розв'язування квадратичної нерівності
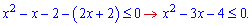
За теоремою Вієта коренями квадратного рівняння будуть x1=4; x2=-1. Оскільки нерівність в нулі виконується -4<0, то розв'язком буде проміжок між коренями. Так як нерівність не строга то краї області включаємо [-1;4].
2) 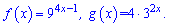
Обчислимо похідні, виконавши попередньо маніпуляції з другою функцією
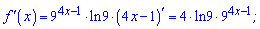
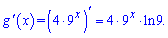
Підставимо похідні в нерівність та спростимо
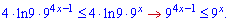
Тут ми спростили на додатній множник (знак нерівності не помінявся). Прирівнюємо показники і розв'язуємо нерівність
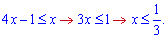
Отримали, що розв'язком буде інтервал від мінус безмежності до однієї третьої, включаючи її.
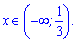
Приклад розв'язано.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Похідна показникової та логарифмічної функцій
- Наступні відповіді - Похідна показникової та логарифмічної функцій. №102
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



