підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 151. Сума всіх біноміальних коефіцієнтів у розкладі бінома 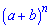 дорівнює 256. Знайдіть степінь
дорівнює 256. Знайдіть степінь 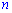 .
.
Розв'язання:
Завдання доволі цікаве і до того просте, якщо знати формулу суми біноміальних коефіцієнтів
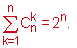
Тоді завдання можемо розв'язати у два рядки
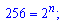
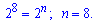
Відповідь: 8.
---===================---
Приклад 152. Сума всіх біноміальних коефіцієнтів, які стоять на парних місцях у розкладі бінома 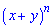 , дорівнює 512. Знайдіть степінь n.
, дорівнює 512. Знайдіть степінь n.
Розв'язання:
Так як суми непарних і парних коефіцієнтів рівні між собою, то маємо залежність
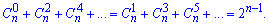
Звідси знаходимо степінь показника
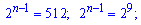
n -1=9; n=10.
Відповідь: 10.
---===================---
Приклад 153. Чому дорівнює сума біноміальних коефіцієнтів розкладу бінома 9 порядку 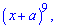 які стоять на непарних місцях?
які стоять на непарних місцях?
Розв'язання:
Використовуємо формулу попереднього прикладу
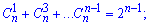
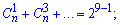
Суму знаходимо піднесенням до двійки до 8 степеня
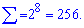
Відповідь: 256.
---===================---
Приклад 154. Доведіть, що сума всіх коефіцієнтів розкладу бінома 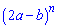 при будь-якому натуральному n дорівнює 1.
при будь-якому натуральному n дорівнює 1.
Розв'язання:
Позначимо a=b=1;тоді формула спроститься до наступної
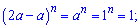
Отже, сума усіх коефіцієнтів рівна одиниці
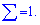
---===================---
Приклад 155. Доведіть, що сума всіх коефіцієнтів розкладу бінома 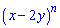 при будь-якому непарному n дорівнює 1.
при будь-якому непарному n дорівнює 1.
Розв'язання:
Розпишемо суму коефіцієнтів при однакових змінних
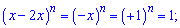
Покладемо х=у=-1 для доведення даного твердження.
Приклад 156. Доведіть тотожність:
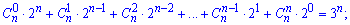
Розв'язання:
Уважно придивіться до розпису розкладу – він відповідає ряду 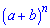 при
при 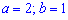 , отже маємо тотожність
, отже маємо тотожність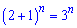 , що і треба було довести.
, що і треба було довести.
---===================---
Приклад 157. Який номер члена у розкладі бінома 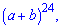 що містить аb у степені 5?
що містить аb у степені 5?
Розв'язання: 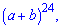
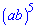
Загальний член розкладу виражається формулою
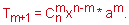
Для даного завдання виписуємо формулу
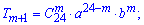
складаємо рівняння
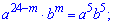
з якого переконуємося, що немає такого члена, оскільки сума показників не рівна степені розкладу
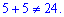
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Біном Ньютона
- Наступні відповіді - Біном Ньютона. №158-163
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



