підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 69. Розв'яжіть показникове рівняння:
Розв'язання:Цей тип показникових рівнянь розв'язують методом виділення основ з однаковими показниками і групуванням множників при них (додавання, віднімання).
1) 4x+1+4x=320
Запишемо ліву частину і вигляді
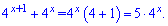
Підставимо у залежність та спростимо
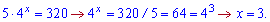
в результаті швидко знаходимо, що х=3 є розв'язком показникового рівняння.
2)3x+2+4*3x-1=279
Розв'язання: Виносимо спільний множник за дужки і сумуємо доданки
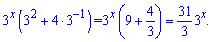
Підставляємо в рівняння та спрощуємо
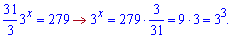
Без проблем знаходимо, що х=3.
3)2*7x+1-6*7x-1-7x=85.
Розв'язання: Виносимо 7x за дужки і сумуюмо все що в дужках.
Далі приходимо до простого показникового рівняння, розв'язком якого є одиниця.
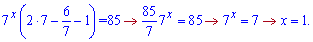
4) 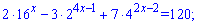
Розв'язання: Схема обчислень попередня, шукаємо найбільший спільний множник та виносимо його з кожного доданку. Все що залишиться - сумуємо
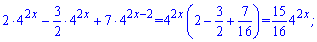
Підстановкою у вихідне рівняння знаходимо
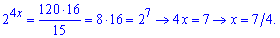
5) 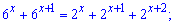
Розв'язання: Групуємо множники при однакових виразах справа та зліва від знаку рівності
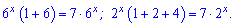
Після підстановки отримаємо
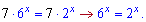
Розв'язуємо за наступною схемою
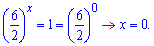
Надалі це правило можете запам'ятати, або інше - будь-яке число в нльовому степені рівне 1.
6) 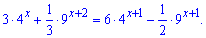
Розв'язання: Переносимо подібні доданки по різні сторони знаку рівності і сумуємо
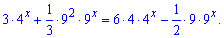
Наступні рівняння розв'язують методом ведення нової змінної.
Приклад 70. Розв'яжіть рівняння:
1) 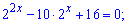
Розв'язання: Позначимо через нову змінну y=2x . Тоді рівняння набуде вигляду
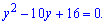
Корені квадратного рівняння знаходимо через дискримінант
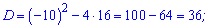
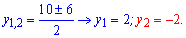
Другий розв'язок до уваги не беремо, тому що додатне число в степені не може бути меншим нуля. Повертаємося до заміни і знаходимо розв'язок показникового рівняння
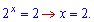
2) 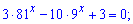
Розв'язання: Яку робити заміну Ви вже мабуть знаєте– це y=9x .
Рівняння при цьому перетвориться на квадратне
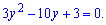
Його корені знаходимо через дискримінант
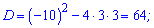
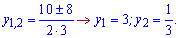
Обидва корені будуть розв'язками. Підставляємо у рівняння і розв'язуємо

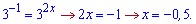
Коренями степеневого рівняння є х=0,5 і х=-0,5.
3)22x+6+2x+7=17.
Розв'язання: Зведемо до класичного вигляду
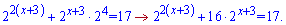
Робимо заміну y=2x+3 та зводимо показникове рівняння до квадратного
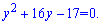
За теоремою Вієта у=1;у=-17.
Другий корінь не має змісту.
Перший підставляємо в заміну і знаходимо х
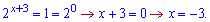
4) 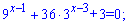
Розв'язання: Заміна проста і випливає з першого доданку y=3x-1 . Перетворимо рівняння
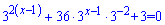
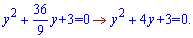
За теоремою Вієта корені рівні у=3; у=1.
Повертаємося до заміни і розв'язуємо
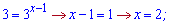
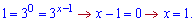
Отримали достатньо прості х=1; х=2 корені показникового рівняння .
5) 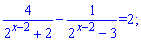
Розв'язання: Дане показникове рівняння розв'язуємо заміною y=2x-2 .
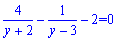
Зводимо до спільного знаменника
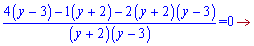
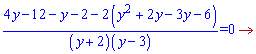
Після групувань отримаємо систему рівнянь
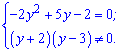
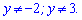
Квадратне рівняння розв'язуємо через дискримінант
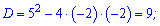
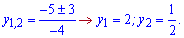
Обидва корені дадуть розв'язки х=1;х=3.
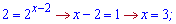
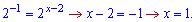
6)2x+22-x=5.
Розв'язання: Перетворимо рівняння
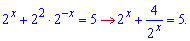
Заміна використовуємо наступну y=2x
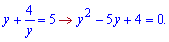
За теоремою Вієта корені квадратного рівняння рівні
у=4;у=1.
Повертаємося до заміни і визначаємо розв'язок показникового рівняння
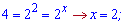
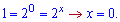
7) 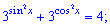
Розв'язання: В показнику маємо тригонометричні функції. Запишемо косинус через синус за теоремою
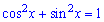
та перетворимо показникове рівняння
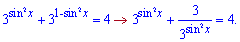
Виконуємо наступну заміну змінних
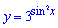
Рівняння перетвориться на квадратне відносно нової змінної
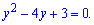
Теорема Вієта дає розв'язки – у=3; у=1.
Повертаємося до заміни і розв'язуємо тригонометричні рівняння
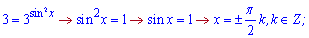
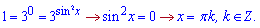
Оскільки другий розв'язок міститься в першому то остаточною відповіддю буде наступна
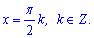
8) 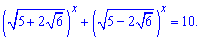
Розв'язання: Показникові рівняння на вигляд складне, але в ньому і подібних використана одна хитрість. Вирази в дужках є спряженими, а їх добуток дає сталу. Це дозволяє виразити одну частину через іншу. В нашому випадку
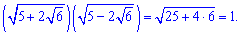
Позначимо 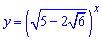 , тоді отримаємо
, тоді отримаємо
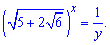
Рівняння зведеться до квадратного
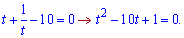
Обчислюємо дискримінант
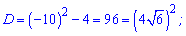
та корені
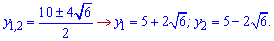
Підставимо в заміну і знайдемо невідомі
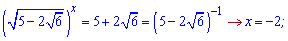
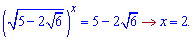
Добре запам'ятайте схему обчислень.
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Показникові рівняння
- Наступні відповіді - Показникові рівняння. № 71-73
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



