підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 75. Розв'яжіть нерівність:
1) 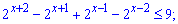
Розв'язання: В цьому прикладі можна піти кількома шляхами. Все залежить від того, який спільний множник Ви винесете. Наприклад, якщо винести 2x то показникова нерівність зведеться до вигляду
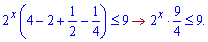
Якщо винести найменший спільний множник 2x-2 , то отримаємо таку нерівність
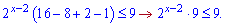
Як поступати вибирати Вам, правильну відповідь отримаєте в обох випадках. Друга візуально простіша, тому продовжимо розв'язувати її
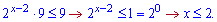
Отримали один інтервал на якому нерівність виконується
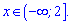
2) 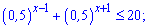
Розв'язання: Винесемо вираз (0,5)x за дужки
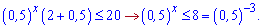
Основа менша одиниці – знак при розкритті нерівності змінюємо на протилежний

Нерівність нестрога тому біля 3 квадратні скобки, нескінченність межі не має тому дужки в таких нерівностях круглі.
3) 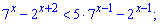
Розв'язання: Переносимо доданки з однаковою основою по одну сторону знаку і групуємо
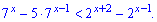
В подібних прикладах старайтеся так групувати доданки, щоб справа і зліва були додатні вирази. Якщо при винесенні за дужки спільних множників отримаєте від'ємні коефіцієнти, то знак нерівності доведеться міняти на протилежний.
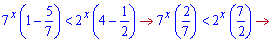
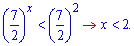
Відповіддю буде один інтервал
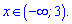
4) 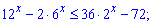
Розв'язання: Тут потрібно скористатися невеликою хитрістю, яку не кожен побачить з першого разу. Доданки потрібно перегрупувати наступним чином
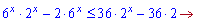
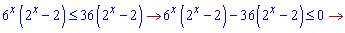
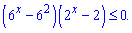
З останнього отримаємо два розв'язки х=2; х=1. Розбиваємо вісь на інтервали і підстановкою нуля встановлюємо знаки функції.
Остаточно розв'язком показникової нерівності є проміжок 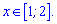
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Показникові нерівності
- Наступні відповіді - Показникові нерівності. №76, 77
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



