ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 76. Розв'яжіть показникову нерівність:
1) 
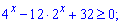
Розв'язання: Цю і наступні нерівності розв'язують введенням нової змінної. Для заданого прикладу вона рівна у=2х.
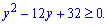
Корені знаходимо через дискримінант
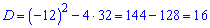
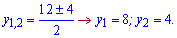
Підставляємо нуль в нерівність і переконуємося, що за межами розв'язків вона виконується (у>8;y<4)
Пригадуємо заміну і знаходимо х
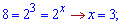
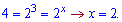
Враховуючи аналіз знаків між коренями, отримаємо два інтервали
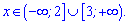
2) 
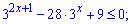
Розв'язання: Розпишемо нерівність
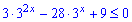
та введемо заміну y=3x
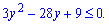
Обчислюємо дискримінант
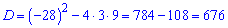
та корені рівняння
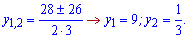
Розділяємо числову вісь даними точками і підстановкою нуля встановлюємо знаки на інтервалах Отримали, що між точками нерівність виконується. Повертаємося до заміни
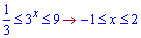
і встановлюємо інтервал
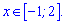
3) 
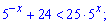
Розв'язання: Переносимо праву сторону нерівності вліво
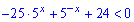
та вводимо змінну y=5x
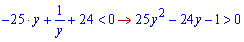
Знаходимо дискримінант
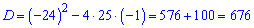
та корені рівняння
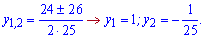
В нулі рівняння від'ємне, тому розв'язки лежать справа та зліва від коренів (y<-1/25; y>1), крім того другий розв'язок не має фізичного змісту.
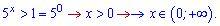
4) 
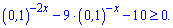
Розв'язання: Введемо нову змінну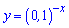 
. Нерівність перетвориться до наступної
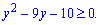
За теоремою Вієта коренями будуть y=10; y=-1.
В нулі функція від'ємна, другий розв'язок не має змісту.
Остаточно отримаємо
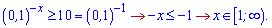
Приклад 77. Розв'яжіть показникову нерівність:
1) 
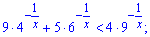
Розв'язання:
Перепишемо нерівність у вигляді
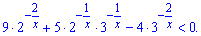
Поділимо на величину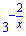 
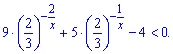
Позначимо за нову змінну
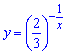
та запишемо квадратну нерівність
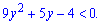
Знаходимо дискримінант
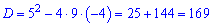
та корені рівняння
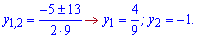
Функція менша нуля між коренями. Другий корінь не має змісту.
З першого кореня отримаємо умову
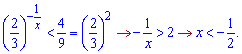
Розв'язком буде інтервал
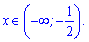
2) 
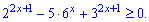
Розв'язання: Проведемо перетворення з наведеною нерівністю та зведемо до вадратичної
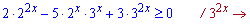
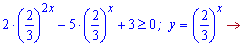
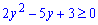
Далі обчислюємо дискримінант
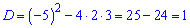
та корені
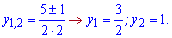
Підстановкою y=0 встановлюємо, що за межами коренів нерівність виконується. Повертаємося до попередньої заміни
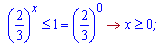
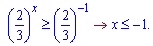
Відповідь міститиме два інтервали
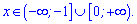
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Показникові нерівності. №75
- Наступні відповіді - Логарифм та його властивості
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
