ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 74. Розв'яжіть нерівність:
1) 
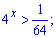
Розв'язання: Перетворюємо праву частину до показника і розв'язуємо
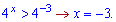
Нерівність виконується при х>-3, тобто змінна повинна належати інтервалу від -3 до плюс безмежності
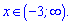
2) 
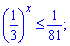
Розв'язання: Приклад аналогічний попередньому. Зводимо нерівність до однієї основи
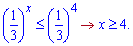
Знак взято протилежний, тому що основа менша одиниці (1/3<1). Отримали у відповідь такий проміжок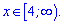 
3) 
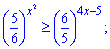
Розв'язання: Перетворимо праву частину нерівності щоб мати однакові основи
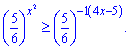
Оскільки основа менша одиниці, то міняємо знак нерівності і розв'язуємо
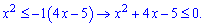
За теоремою Вієта коренями квадратного рівняння будуть х=-5; х=1.
Щоб ефективно і швидко знаходити проміжки на яких функція квадратного рівняння приймає знак "+" або "-" завжди користуйтесь правилом:
Підставляйте нуль – змінні зануляться і лишається вільний член. Дальше запам'ятайте, що знаки у випадку квадратичних функцій чи поліномів чергуються. В нашому випадку проміжок [-5;1] містить 0 і має від'ємний знак функція, що і вимагає нерівність. Тобто проміжок між коренями є розв'язком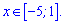 
, за його межами знак протилежний ("+").
4) 
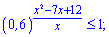
Розв'язання: Не лякайтесь одиниці, її завжди можна представити як основу в нульовому степені.
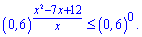
Далі, оскільки основа менша одиниці – міняємо знак нерівності і знаходимо потрібний проміжок
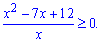
Корені квадратного рівняння згідно теореми Вієта рівні
х=4;х=3.
Не забуваємо, що потрібно виключити з розв'язку точку х=0 в якій знаменник рівний нулеві. Підстановкою нуля в квадратне рівняння отримуємо, що на (0;3) та від 4 до безмежності знак функції додатній
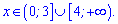
5) 
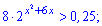
Розв'язання: Перетворимо показникову нерівність
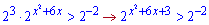
Порівнюємо степені
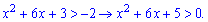
Корені за теоремою Вієта будуть рівні х=-5;х=-1. В нулі функція додатна, причому нуль не міститься в інтервалі між коренями квадратного рівняння.
Звідси розв'язком є два інтервали
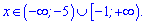
6) 
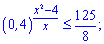
Розв'язання: Виконаємо маніпуляції з нерівністю
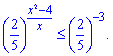
Основа менша одиниці, тому знак змінюємо на протилежний
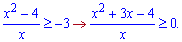
Коренями квадратного рівняння будуть х=-4;х=1. Також виключаємо 0 з розв'язків. Розбиваємо дійсну вісь на 4 інтервали і встановлюємо знак, для цього підставляємо точки з інтервалу.
В результаті отримаємо 2 проміжки де нерівність виконується
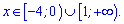
7) 
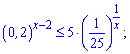
Розв'язання: Перетворимо нерівність
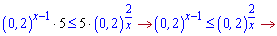
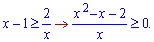
За теоремою Вієта знаходимо корені х=2; х=-1. В точці 0 функція міняє знак. В нулі квадратне рівняння від'ємне, а це значить, що розв'язком показникової нерівності є 2 інтервали
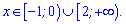
8) 
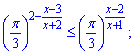
Розв'язання: Почати аналіз слід з того, що основа більша одиниці, оскільки Pi=3,14 при діленні на 3 дасть таке значення 1,047. Тому при однакових основах порівнюємо показники
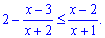
Переносимо по одну сторону від знаку і зводимо до спільного знаменника дроби
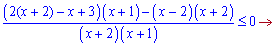
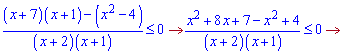
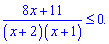
Отримали три точки, які розділяють дійсну вісь на інтервали,
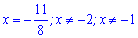
причому перша лежить між двома наступними. Підстановкою нуля встановлюємо, що при х>-1 функція додатна. Рядом на інтервалах знаки чергуються. Остаточно отримаємо дві ділянки де виконується нерівність
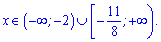
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Показникові рівняння. № 71-73
- Наступні відповіді - Показникові нерівності. №75
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
