ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 46. Знайдіть проміжки зростання і спадання функції:
1) 
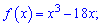
Розв'язання:
Обчислюємо похідну функції
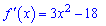
та прирівнюємо її до нуля
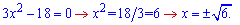
Будуємо числову вісь і встановлюємо знак похідної підстановкою точок з інтервалу. За правило, використовуйте точку 0 або інші прості точки, в яких легко перевірити знак похідної. Далі, якщо не має інших особливих точок знак функції чергується на сусідніх проміжках.
Перевіряємо знак похідної
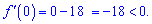
Отже між коренями функція спадає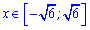 
та зростає за межами цього проміжку
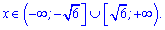
Для наочності графік функції наведено нижче.
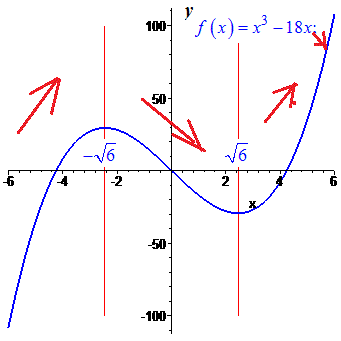
2) 
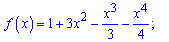
Розв'язання:
Знаходимо похідну полінома
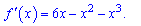
З умови рівності нулю похідної визначаємо критичні точки
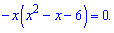
Перший корінь рівний нулю x=0, інші знаходимо за теоремою Вієта x=-3; x=2.
В одиниці похідна додатна
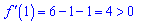
а значить функція зростає, на сусідніх проміжках знак похідної чергується. Числова вісь із встановленими знаками похідної матиме вигляд.
Бачимо, що отримали два проміжки зростання функції
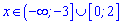
та два на яких функція спадає
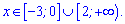
Графік функції наведено нижче
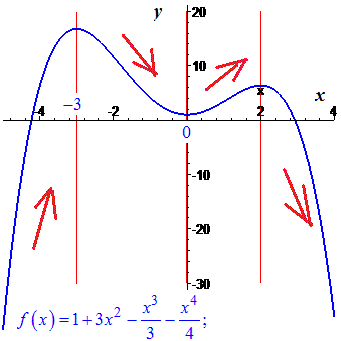
3) 
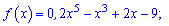
Розв'язання:
Шукаємо похідну функції
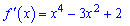
та прирівнюємо її до нуля
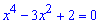
Отримали біквадратне рівняння. Заміною змінних t=x2 зводимо його до квадратного
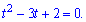
За теоремою Вієта коренями будуть t=1; t=2.
Повертаємося до заміни і визначаємо критичні точки
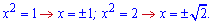
Коефіцієнт при x4 більший нуля, значить при великих значеннях змінної похідна більша нуля. На проміжках лівіше знаки похідної чергуються. Наносимо критичні точки та значення похідної на числову вісь
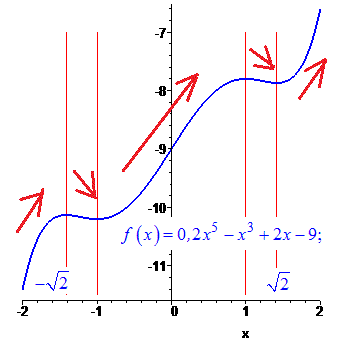
Отримали три проміжки зростання функції
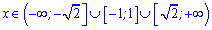
та два проміжки спадання
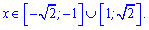
Графік функції наведено на рисунку
4) 
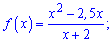
Розв'язання:
Задана дробова функція. ОДЗ – вся дійсна вісь крім нуля знаменника
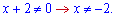
Обчислюємо похідну від частки за правилом
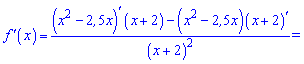
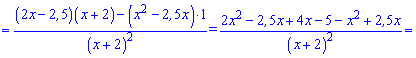
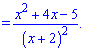
Знаходимо нулі чисельника
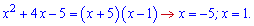
Знайдені точки разом з ОДЗ наносимо на числову вісь і встановлюємо знаки похідної
При переходи через (-2) похідна не змінює знак, це зумовлено Тим , що знаменник міститься в парному степені.
Функція зростає на двох крайніх інтервалах
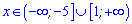
та спадає посередині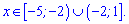 
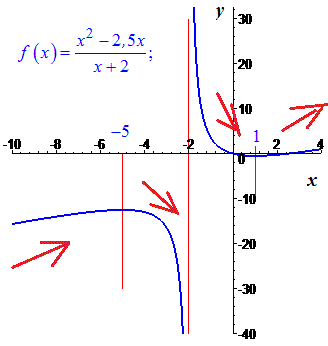
Графік функції наведено нижче
5) 
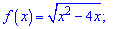
Розв'язання:
Встановлюємо область допустимих значень
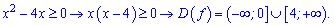
Дальше визначаємо критичні точки
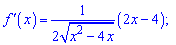
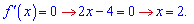
При більших значеннях аргумента (x>2) похідна додатна, при менших – від'ємна. Разом з ОДЗ це дасть наступний інтервал зростання функції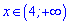 
та спадання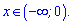 
Якщо не враховувати ОДЗ то можна отримати зайві результати, тому за цим слідкуйте. На тестуванні таких проступків від Вас і чекають, том завдання, як правило, підбирають каверзні.
Графік функції зображено нижче
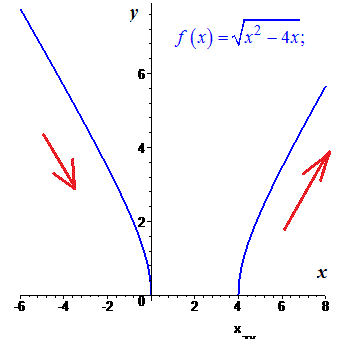
6) 
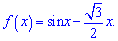
Розв'язання:
Функція визначена на множині дійсних чисел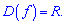 
Обчислюємо похідну функції
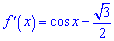
та прирівнюємо до нуля
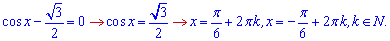
Так як косинус періодична функція то отримаємо безліч проміжків зростання
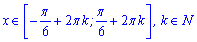
та проміжків спадання функції
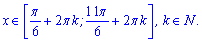
Фрагмент графіку періодичної функції зображено нижче
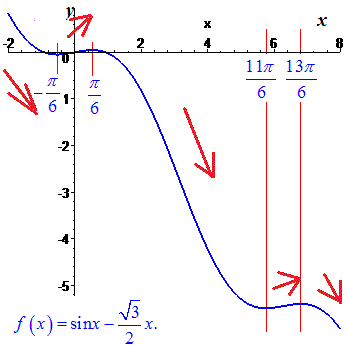
Ось такий для когось простий, а для когось не дуже аналіз функції дозволить знайти точки підозрілі на екстремум, а також встановити інтервали зростання та спадання функцій.
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Механічний зміст похідної
- Наступні відповіді - Ознаки зростання і спадання функції. №47-49
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
