підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
1 Варіант
Приклад 47. Доведіть, що функція
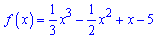
зростає на множині дійсних чисел.
Розв'язання:
ОДЗ вся дійсна вісь. Обчислюємо похідну
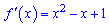
та прирівнюємо до нуля
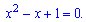
Обчислюємо дискримінант
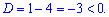
Він менший нуля, тобто функція не має критичних точок. Іншими словами – вона або всюди зростає, або навпаки – спадає.
Встановимо знак похідної
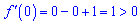
вона більша нуля. Значить функція зростає на множині дійсних чисел. Вихідне твердження доведено.
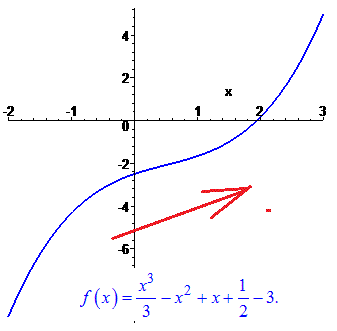
Приклад 48. Доведіть, що функція
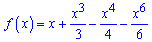
спадає на проміжку 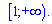
Розв'язання:
ОДЗ функції вся дійсна вісь.
Обчислюємо похідну функції
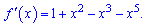
З умови рівності нулю похідної визначаємо критичні точки
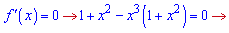
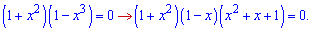
Перша і остання дужка завжди більші нуля
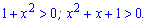
Із середньої знаходимо критичну точку
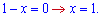
Оскільки в завданні запитують про характер функції справа від одиниці, то перевіряємо знак похідної, наприклад в точці 2
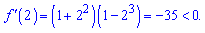
Отримали від'ємне значення, отже функція спадає на проміжку від одиниці до безмежності 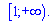
Без обчислення з самого вигляду функції було ясно, що функція спадає при великих значеннях змінної, оскільки коефіцієнт при найстаршому степені від'ємний (-1/6). Потрібно тільки встановити точку максимуму, що ми і зробили через похідну.
Графік функції має наступний вигляд
Приклад 49. Знайдіть, при яких значеннях a зростає на R функція:
1) 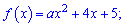
Розв'язання:
Шукаємо похідну функції
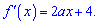
Щоб функція зростала на множині дійсних чисел необхідно, щоб вона не мала точок екстремуму, а знак похідної був всюди додатнім. З цієї умови маємо
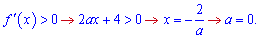
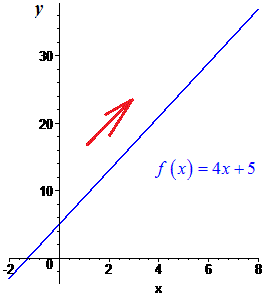
Квадратична функція при a=0 перетворюється в рівняння прямої f(x)=4x+5.
Графік наведено нижче
2) 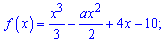
Розв'язання:
Похідна прийме значення
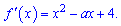
Прирівнявши до нуля, отримаємо квадратне рівняння з параметром
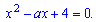
Дискримінант повинен бути менший нуля
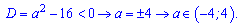
Отримали , що параметр a повинен належати інтервалу (-4;4).
3) 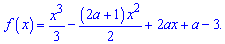
Розв'язання:
Обчислюємо похідну функції та прирівнюємо її до нуля
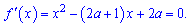
Дискримінант буде рівний
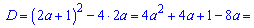
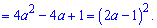
Корені рівняння
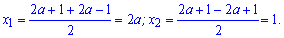
Щоб корені стягнути в одну точку потрібно покласти
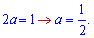
Похідна тоді всюди додатна крім точки 1, де перетворюється в нуль.
Графік функції наведено нижче.
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Ознаки зростання і спадання функції
- Наступні відповіді - Точки екстремуму функції
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



