ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 95. Розв'яжіть нерівність:
1) 
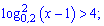
Розв'язання. ОДЗ нерівності буде інтервал
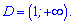
Переносимо 4 до логарифма і розписуємо через різницю квадратів
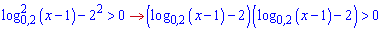
Розписуємо кожну з дужок, враховуючи, що вони додатні.
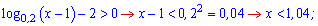
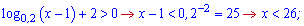
Від'ємні значення в дужках немає змісту розглядати, оскільки це суперечитиме з ОДЗ. Спільним останніх двох розв'язків з ОДЗ є наступний інтервал
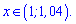
Він і є розв'язком логарифмічної нерівності.
2) 
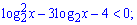
Розв'язання. З вигляду нерівності бачимо, що її необхідно звести до квадратного рівняння заміною 
. Перед цим випишемо область допустимих значень логарифма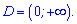 
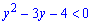
Теорема Вієта дає такі корені y=4; y=-1.
В нулі нерівність виконується -4<0, отже розв'язком квадратичної нерівності буде інтервал
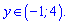
Але це ще не кінець обчислень, не забуваємо повернутися до заміни і знайти обмеження на логарифмічну нерівність
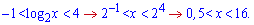
Останній інтервал
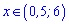
повністю належить ОДЗ, тобто є розв'язком нерівності.
3) 
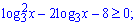
Розв'язання. Рівняння за схемою розв'язання ідентичне попередньому. ОДЗ в нього вся додатна вісь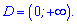
Заміною змінних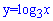 
нерівність зводимо до квадратичної
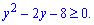
Перебором можливих варіантів коренів встановлюємо, що підходять тільки y=4; y=-2.
Теорема Вієта це підтверджує
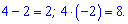
Підстановкою нуля в нерівність знаходимо, що вона виконується за межами проміжку між коренями
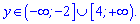
Заміна, яку виконали вище перетворить отримані результати в наступні
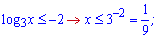
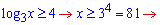
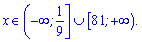
Не забуваємо про область допустимих значень, вона дещо звузить множину розв'язків нерівності
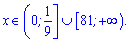
4) 
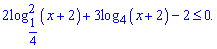
Розв'язання. Область визначення функцій в нерівності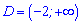 
.
Дальше є два шляхи: переходити до основи 4, тоді знак в першому доданку змінюємо на від'ємний;
Або до основи 1/4, знак змінюємо на протилежний перед другим доданком за правилом
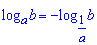
Це потрібно, щоб рівняння мало одну основу і дальше було зручно обчислювати.
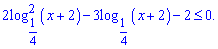
Виконуємо заміну змінних та зводимо до квадратичної нерівності
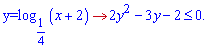
Дискримінант рівний
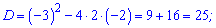
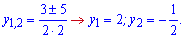
Підстановкою нуля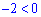 
переконуємося, що розв'язок нерівності відносно y лежить між знайденими коренями
.
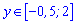Вертаючись до заміни, отримаємо
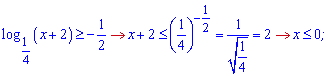
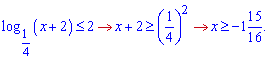
Враховуючи всі знайдені обмеження остаточний розв'язок логарифмічної нерівності записуємо у вигляді проміжку
-------------------------------------------------------------
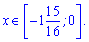
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Логарифмічні нерівності. №94
- Наступні відповіді - Логарифмічні нерівності. №96, 97
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
