підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 87. Побудуйте графік функції:
1) 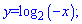
Розв'язання:
Область визначення функції

буде ліва півплощина 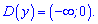
Виходячи з вигляду функції, графіком буде логарифм симетрично відображений відносно осі ординат.
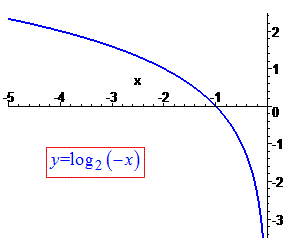
2) 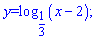
Розв'язання:
Область визначення логарифма
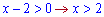
будуть всі змінні, які більші двійки 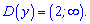
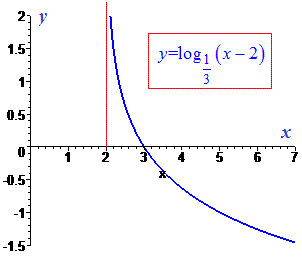
Оскільки основа менша одиниці, то графік буде симетричний в порівнянні до стандартного логарифма відносно осі абсцис і перетинатиме цю вісь в точці
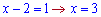
з ординатою =3.
Графік функції зображено на рисунку
3) 
Розв'язання:
Функція логарифм від модуля аргументу x визначена всюди, крім точки нуль
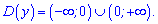
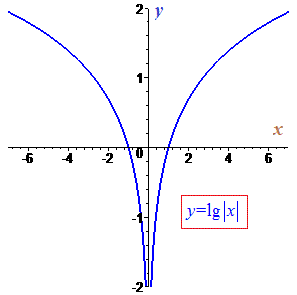
Графік утворюється симетричним поворотом стандартного логарифма навколо осі Oy. В точках x=1;x=-1 логарифм перетинається з віссю абсцис. Графік функції зображено на рисунку нижче.
4) 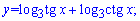
Розв'язання:
Встановлюємо точки в яких тангенс та котангенс не існують. Ними будуть наступні
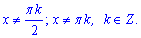
Перепишемо функцію, використавши властивість суми логарифмів
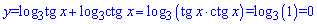
Функція рівна нулю на всій дійсній осі за винятком точок в яких тангенс та котангенс не існують. Графік функції зображено на рисунку нижче

5) 
Розв'язання:
Завдання дуже цікаве, оскільки функція має два обмеження:
перше – синус повинен бути більший нуля;
друге – корінь квадратний можна взяти лише від невід'ємного числа, звідси слідує, що логарифм функція повинна бути не меншою за нуль. Все це можливо тільки за умови, що синус рівний одиниці. Відповідно логарифм одиниці рівний нулеві, з якого можна взяти корінь.
Тому єдиним розв'язком будуть точки
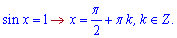
Графік наведено нижче.

6) 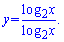
Розв'язання:
Візуально виглядає, що графіком функції буде одиниця. Проте це не так. За означенням логарифма маємо перше обмеження x>0. Крім того за властивістю дробу на нуль ділити не можна, а заданий знаменник перетворюється в нуль коли x=1. Цю точку з графіку виключаємо і остаточно отримуємо такий кінцевий результат

-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Логарифмічна функція та її властивості
- Наступні відповіді - Логарифмічні рівняння
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



