підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 83. Знайдіть область визначення логарифмічної функції:
1) 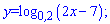
Розв'язання:
Застосовуючи властивість логарифма область визначення логарифма знаходимо з нерівності
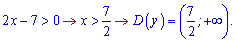
2) 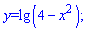
Розв'язання:
Розв'язуємо нерівність
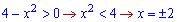
та встановлюємо знаки на інтервалах.
Між коренями виконуються умови нерівності, відповідно вона і буде областю визначення
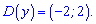
3) 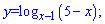
Розв'язання:
За властивістю логарифма маємо систему нерівностей для визначення області визначення
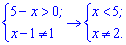
Відповіддю будуть два інтервали
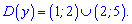
4) 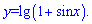
Розв'язання:
Виписуємо нерівність

Оскільки синус функція для всіх більша за -1, і тільки в одній точці їй рівня, то цю точку виключаємо з області визначення
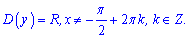
---==================---
Приклад 84. Порівняйте з нулем логарифм:
1) 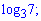
Розв'язання:
Для визначення знаку уявіть собі, що справа за знаком рівності стоїть невідома і розв'яжіть логарифм відносно неї
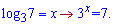
Останнє можливо, якщо x>0, тобто логарифм більший за нуль

2) 
Розв'язання:
Розв'язуємо аналогічним чином, записуємо логарифм у вигляді
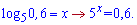
Останнє можливо при від'ємному показнику, тобто вираз менший нуля
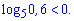
3) 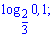
Розв'язання:
Перетворюємо логарифм
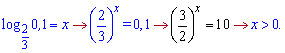
Чорним виділено результат ділення одиниці на попередній вираз. Якщо маєте сумніви в правильності знаків чи відповіді, то краще звести до відомого простого випадку. Логарифм більший нуля
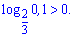
4) 
Розв'язання:
Розв'язуємо за відомою схемою.
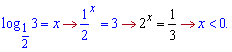
Тут використана схема попереднього завдання, тобто ділення одиниці на логарифм. В результаті отримали, що він менший нуля.
---==================---
Приклад 85. Порівняйте числа а і b, якщо відомі їх логарифми:
1) 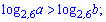
Розв'язання:
За властивістю логарифмів при основі більшій за одиницю більшому значенню логарифма відповідає більше число. Звідси a>b.
2) 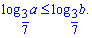
Розв'язання:
Основа менша одиниці (3/7<1), отже меншому числу відповідає більше значення логарифма. Знак змінюємо на протилежний 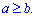
---==================---
Приклад 86. Порівняйте з одиницею основу логарифма, якщо задано нерівності:
1) 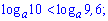
Розв'язання:
За властивістю логарифма, яка описана вище, основа повинна бути меншою від одиниці (a<1).
2) 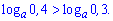
Розв'язання:
Дана нерівність виконується при основі більшій одиниці (a>1).
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Логарифм та його властивості. №80- 82
- Наступні відповіді - Логарифмічна функція та її властивості. №87
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



