З уроку навчимося знаходити умовні екстремуми прямим методом виключення змінних та методом множника Лагранжа. Локальні екстремуми функції багатьох змінних коли її аргументи є незалежними змінними називають безумовними екстремумами. Крім безумовних є ще умовні екстремуми – це такі, які шукають не у всій області визначення, а за певних обмежень (умов) на аргументи функції.
Нехай маємо в області D функцію двох змінних f(x,y) і контур Γ, яка задана рівнянням φ(x,y)=0 та знаходиться в D.
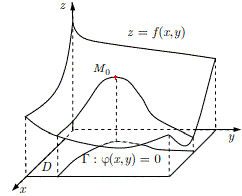
Стоїть задача у визначенні на лінії Г стаціонарної точки M0(x0;y0), в якій функція f(x,y) досягає максимуму або мінімуму (при обході координат φ(x,y)=0).
Залежність φ(x,y)=0 називають рівнянням зв'язку або зв'язком.
За умов зв'язку точка M0(x0;y0) називається точкою локального умовного максимуму [мінімуму] функції z=f(x,y), якщо знайдеться окіл точки U(M0) в якому для всіх точок M∈U(M0) виконується нерівність
f(M)≤ f(M0)
[f(M)≥f(M0)].
Сьогодні навчимося розв'язувати завдання на знаходження екстремумів функції z=f(x,y) за умови φ(x,y)=0 методом виключення змінних та методом Лагранжа.
Метод виключення змінних знаходження умовного екстремуму
Метод виключення змінних застосовують у випадках коли з рівняння зв'язку φ(x,y)=0 змінну y можна виразити в явному вигляді y=y(х). ( Або навпаки, x=х(y)).
Тоді функцію z=f(x,y) можна переписати як функцію однієї змінної
z=f(x,y(х)).
Далі методика один в один повторює обчислення локального екстремуму.
обчислюємо похідну від z по х та прирівнюємо до нуля.
dz/dx=df(x,y(х))/dx=0.
Знайдена точка M0(x0;y(x0)) і буде умовним екстремумом z=f(x,y) знайденим методом виключення змінних.
На практиці знаходження умовного екстремуму за цією схемою називають прямим методом виключення змінних.
Приклад 1. Знайти екстремум функції z=7+3x2-6y, якщо її аргументи задовольняють рівняння y-2x=0.
Розв'язування: В даному завданні бачимо, що умову зв'язку y-2x=0 можна записати у вигляді y=2x і знайти точку умовного екстремуму можемо прямим методом виключення змінних.
Підставимо y=2x у z(x,y):
z=7+3x 2-6y=7+3x2-6•2x=7+3x2-12x.
Обчислимо похідну за змінною "ікс» та прирівняємо її до нуля.
dz/dx=3•2x-12=6x-12=0,
звідси x0=12/6=2.
Знайдемо y0 з рівняння зв'язку y=2x:
y0=2•x0=2•2=4.
Сама функція приймає значення
z=7+3•22-6•4=7+12-24=-5.
Друга похідна d2/dx2=6>0, отже точка M0(2;4) є точка умовного мінімуму для функції z=7+3x2-6y за умови y-2x=0 і досягає значення zmin=-5.
Приклад 2. Знайти екстремум функції z=x+3y2 відносно функції зв'язку y+5x=0.
Розв'язування: Умову зв'язку 5y+x=0 запишемо у вигляді явної функції
x=-5y.
Точку умовного екстремуму знайдемо методом виключення змінних.
Підставимо x=-5y у функцію z=x+3y2:
z=x+3y2=-5y+3y2.
Похідну за змінною "ігрик» прирівняємо до нуля.
dz/dy=-5+3•2y=-5+6y;
dz/dy=0; -5+6y =0;
y0=5/6;
звідси x0=-5y=-5•5/6=-25/6.
Обчислимо значення функції в особливій точці M0(-25/6;5/6):
z0=x+3y2=-25/6+3•(5/6)2=25/3.
Друга похідна d2z/dy2=6>0, отже знайдена точка M0(-25/6; 5/6) є точкою умовного мінімуму для функції z(x,y)=x+3y2 при зв'язку 5y+x=0.
Умовно мінімальне значення функції zmin=25/3.
Пам'ятайте наступне!
Уважно перегляньте, що можливо виражати умову зв'язку x=x(y), а не тільки y=y(x). Але зважайте, що це впливає на хід обчислення похідної. Для зв'язку у вигляді рівняння прямої, чи параболи це немає значення, а от для логарифма, тригонометричних функцій похідна важлива.
Також при зв'язку x=x(y) не забувайте, що в записі M0(x0;y0) першою йде точка x0, далі y0, хоча знаходимо їх у зворотному порядку.
Приклад 3. Знайти екстремум функції z=ln(x)-exp(y), якщо її аргументи задовольняють рівняння y-ln(x3)=0.
Розв'язування: Рівняння зв'язку y-ln(x3)=0 запишемо у вигляді явної функції
y=ln(x3).
Підставимо умову y=ln(x3)у функцію z=ln(x)-exp(y):
z=ln(x)-exp(ln(x3))=ln(x)-x3.
Обчислюємо похідну за змінною "ікс» функції z
dz/dx=1/x-3x2.
Прирівнюємо знайдену похідну до нуля та визначаємо стаціонарну точку
dz/dx =0; 1/x-3x2=0;
x≠0;1-3x3=0.
x3=1/3; x0=1/31/3
y0=ln(x03)=ln(1/3).
Друга похідна d2z/dx2=-1/x2-6x<0, отже знайдена точка M0(1/31/3; ln(1/3)) є точкою умовного максимуму для функції z(x,y)=ln(x)-exp(y) за умови y-ln(x3)=0.
В точці умовного екстремума функція приймає значення
zmax=ln(1/31/3)+exp(ln(1/3))=1/3+ 1/3•ln(1/3).
Тут при розписі виразу використали властивості логарифма
ln(ab)=b•ln(a);
exp(ln(a))=a.
Далі познайомимося зі схемою обчислень методу Лагранжа. Теорію та більше готових завдань на умовний екстремум методом Лагранжа розглянемо на наступному уроці.
Приклад 4. (416) Знайти екстремум функції z=x2+y2-xy+x+y-4, якщо x+y+3=0.
Розв'язання: Складемо функцію Лагранжа L(x,y,λ)= x2+y2-xy+x+y-4+ λ (x+y+3).
Це не важко зробити, якщо поглянути, що нам задано в умові.
Знайдемо частинні похідні І порядку функції L(x,y,λ) за аргументами x,y:
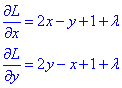
Частинні похідні функції Лагранжа потрібні для побудови системи трьох лінійних алгебраїчних рівнянь (СЛАР) відносно трьох невідомих x0, y0, λ за формулами (3):
Третє рівняння СЛАР це сама умова зв'язку x+y+3=0. Розв'язуємо систему рівнянь
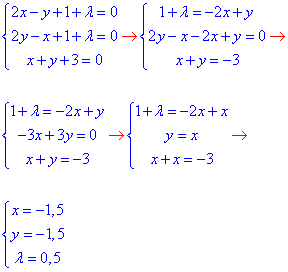
Після розкриття СЛАР та визначення стаціонарної точки M0(-1,5;-1,5) знаходимо значення самої функції
z=(-1,5)2+(-1,5)2-(-1,5)•(-1,5)+(-1,5)-4=-4,75.
Далі потрібно визначити чи маємо точку умовного максимуму чи мінімуму, а для цього потрібно знайти диференціал функції Лагранжа 2 порядку в стаціонарній точці.
Для його обчислення знайдемо частинні похідні ІІ порядку функції L(x,y,λ) та підставимо в формулу другого диференціалу:
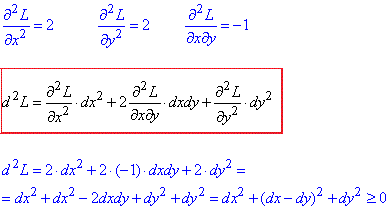
Оскільки d2L містить суми квадратів, то він додатний d2L≥0, і робимо висновок, що точка M0(-1,5;-1,5) є точкою умовного мінімуму функції z=x2+y2-xy+x+y-4, і мінімальне значення
zmin=-4,75.
На наступному уроці розберемо 5 прикладів на метод Лагранжа та саму теорію знаходження умовного екстремуму цим способом.


