Часто на практиці зустрічаються функції, в яких незалежна змінна x і функція y зв'язані між собою формулою
f(x,y)=0
з якої не можна відокремити саму функцію. В цьому випадку функція y(x) називається неявною функцією від аргумента x.
Однак саму похідну від функції по змінній x можна обчислити. Для цього диференціюють функцію f(x,y) по x, при цьому враховують, що сама функція залежна від змінної y=y(x). З одержаного рівняння згруповують доданки, що містяться при похідній y' і виражають її.
Як це виглядає на пракиці проілюстровано на прикладах із Дубовика В.П., Юрика І.І. "Вища математика. Збірник задач".
Приклад 1. Знайти похідні неявно від заданих функцій y(x) .
1) (5.219) 3x+3y=3x-y
Розв'язок:Продиференціюємо праву і ліву частини
![]()
![]()
Отриманий вираз поділимо на спільний множник ln(3) та згрупуємо доданки, що містять похідну y'(x) і перенесемо їх в одну сторону за знак рівності. В результаті отримаємо
![]()
Поділивши на множник при похідній y'(x) отримаємо її значення
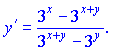
Для спрощення винесемо із чисельника та знаменника спільні множники 3x та 3y відповідно. В результаті отримаємо:
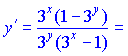
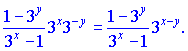
Як бачите, нічого складного ми не робили, проте швидко відшукали похідну неявно заданої функції. Розглянемо наступне завдання.
2) (5.223)![]()
Розв'язок:Проведемо диференціювання виразу. Перший доданок дасть 2, похідну від арккосинуса знаходимо за правилом складеної фунції
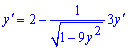
Виділяємо доданки, що містять похідну y'(x)
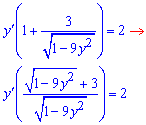
Поділимо на множник при похідній та відшукаємо її значення
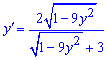
Завдання повністю розв'язане.
3) (5.227)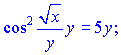
Розв'язок:Обчислимо похідну правої і лівої частини, від косинуса знаходимо, як від складеної функції
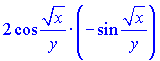
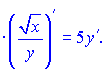
Похідну від частки функцій рівна
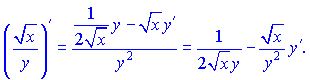
Перших два множники рівні синусу подвійного кута. Тому похідні можемо згрупувати у вигляді
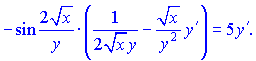
Домножимо праву та ліву частини на множник ![]() , щоб позбутися знаменників та згрупуємо доданки при похідній y'(x)
, щоб позбутися знаменників та згрупуємо доданки при похідній y'(x)
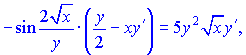
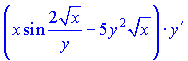
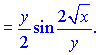
З останньої залежності знаходимо значення потрібної похідної
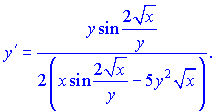
В такого роду прикладах головне не помилитися при відшуканні похідних. Фугкції тут взято доволі складні, заодно вивчете інші правила диференціювання.
4) (5.236)![]()
Розв'язок:Диференціюємо неявно задану функцію по змінній
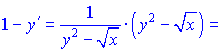
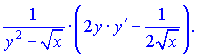
Перегрупуємо доданки, що містять y'
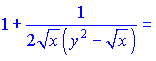
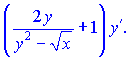
Зводимо вирази до спільного знаменника
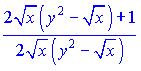
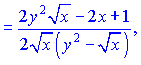
та підставляємо їх на свої місця
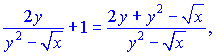
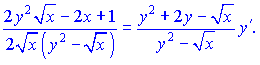
Звідси виражаємо похідну функції
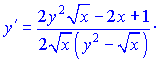
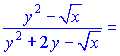
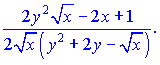
На цьому завдання розв'язано.
При обчисленні похідної неявно заданої функції типовими помилками на практиці є неправильне взяття похідної та плутанина зі знаками при групуванні подібних доданків. Будьте уважні в таких ситуаціях та не допускайте помилок. На скадних умовах Ви побачили як брати похідну від неявно заданої функцій, тому, якщо попрацюєте самостійно, то з даної теми отримаєте хороші результати на тастах, контрольних.


