Метод логарифмічного диференціювання стає в нагоді при диференціюванні добутку кількох функцій або їх частки. Його зручно застосовувати при дифенеціюванні виразів, що містять корені із дробів (функцій), а також коли показник функції також являє собою складену функцію y=f(x)g(x)
В таких випадках доцільно обидві частини виразу спочатку прологарифмувати за експонентою (e), а потім приступити до диференціювання. Цей спосіб одержав назву логарифмічного диференціювання. Похідну від логарифма функції називають логарифмічною похідною. Суть методу за допомогою формул можна описати наступним чином:
маємо складну функцію вигляду y=t(x);
до обох сторін застосовуємо логарифмування
ln(y)=ln(t(x))
і знаходимо похідні правої і лівої частини рівності у вигляді формул
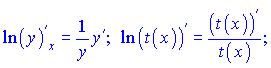
Прирівнюємо похідні і виражаємо y'
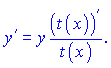
В цьому вся суть методу, далі все залежить від функції t(x).
Якщо t(x) задана добутком функцій
![]()
то за властивостями логарифма при диференціюванні отримаємо суму логарифмів
![]()
Якщо маємо дробову функцію
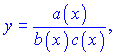
то, застосовуючи логарифмування, отримаємо різницю логарифмів
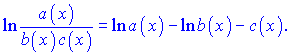
Якщо маємо складену показникову функцію (функція в степені іншої)
![]()
то за властивостями логарифма отримаємо залежність
![]()
У випадку коренів (g(x)=С=1/2; 1/3, ...) диференціювання значно спрощується і отриамємо добуток показника на огарифм
![]()
Подальше обчислення похідних залежить від складності самих функцій. Розглянемо конкретні завдання, щоб даний матеріал став для Вас більш зрозумілішим і наочнішим.
Приклад 1. Використовуючи логарифмування знайти похідну
(Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" )
1) (5.2.178) y=x5x
Розв'язок. Приклади вибрано складні для того, щоб розкрити всю силу методу логарифмічного диференціювання та розглянути поширені для студентсьої практики приклади. Проведемо логарифмування лівої і правої частин
![]()
Далі знайдемо похідну добутку функцій
![]()
![]()
Похідна лівої частини показана при викладі теоретичного матеріалу. Записуємо результати обчислень
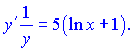
Далі переносимо функцію y із знаменника в праву частину та не забуваємо замінити її значення на вихідне
![]()
Незважаючи на складний вигляд даний приклад розв'язано.
2) (5.2.191)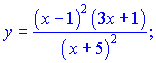
Розв'язок.Знаходимо логарифм дробової функції
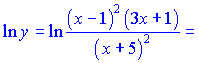
![]()
Проводимо диференціювання обох частин залежності
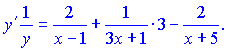
Зведемо під спільний знаменник праву сторону. В результаті математичних операцій отримаємо
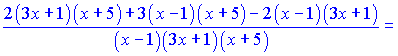
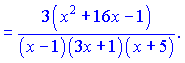
Підставимо в вихідну формулу, перенісши функцію в праву частину
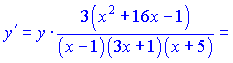
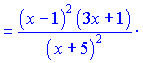
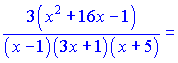
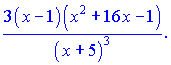
В результаті ряду нескладних маніпуляцій отримали досить компактний кінцевий результат похідної. При обчисленні даного прикладу напряму подібний результат довелося б шукати дуже довго.
3) (5.2.195)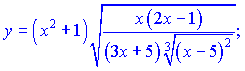
Розв'язок.Незважаючи на складний вигляд, дану функцію на основі властивостей поазників можна переписати у вигляді
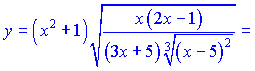
![]()
![]()
Застосуємо логарифмування
![]()
![]()
Похідна від правої частини рівна
![]()
![]()
![]()
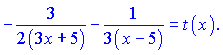
Тут для спрощення подальших викладок позначии резуьтат диференціювання через t(x).
Враховуючи похідну від ln(y), остаточно отримаємо
![]()
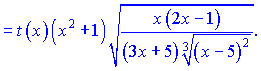
Можна залишати в такому вигляді, оскільки суть даного уроку навчитися застосовувати метод логарифмічного диференціювання. Проте, якщо Ви захочете для спрощення звести все до спільного знаменника, то отримаєте таку відповідь
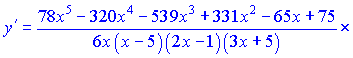
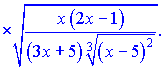
Повірте - це займе у Вас чимало часу
4) (5.2.199)![]()
Розв'язок.Проводимо логарифмування функції
![]()
![]()
Далі за наведеною схемою знаходимо диференціюємо праву частину залежності
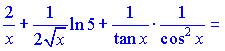
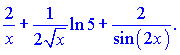
Підставивши в формулу для похідної від логарифма, отримаємо
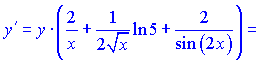
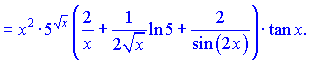
На цьому розв'язування прикладу завершено.
Практикуйте з подібними завданнями і через певний час у Вас не буде жодних труднощів із знаходженням похідної через огарифмування функції.


