В геометрії, механіці, фізиці часто зустрічається параметричний спосіб задання рівняння, що описує криву на площині чи в просторі. Саму ж лінію можна розглядати як геометричне місце послідовних положень рухомої точки, координати x та y якої є функціями допоміжної змінної 
(часу, швидкості, відстані і т.д.) Допоміжну змінну називають параметром, а рівняння функції – параметричним рівнянням. Для прикладу, крива на площині визначається двома рівняннями
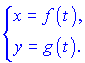
Похідна параметричної функції першого порядку знаходиться за правилом
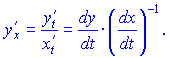
Друга похідна параметрично заданої функції визначається залежністю
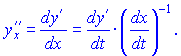
Аналогічним чином можна вивести похідні старших порядів.
Розглянемо декілька прикладів для закріплення матеріалу на практиці.
Приклад 1. Знайти похідні функцій , заданих параметрично.
(Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" )
1) (5.253)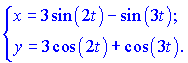 
Розв'язок. Обчислимо похідні функції та аргументу за параметром t
Знайдені значення підставляємо у формулу похідної
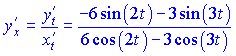
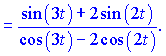
В даному випадку, щоб не виносити знак мінус перед дріб, домножили на (-1) знаменник та переставили доданки так, щоб першими йшли додатні. Сама ж крива на площині матиме вигляд
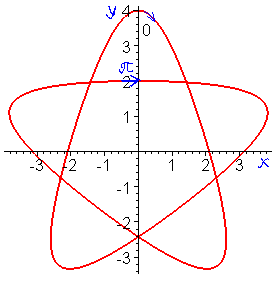
2) (5.256)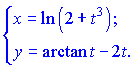 
Розв'язок. Обчислюємо похідні x,y за параметром
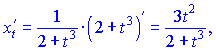
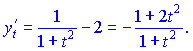
Обчислюємо значення похідної 
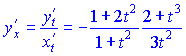
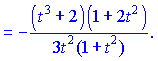
Приклад не складний, головне правильно знайти похідні логарифма та арктангенса.
3) (5.261)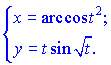 
Розв'язок.Знходимо похідні сладених функцій
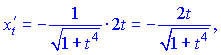
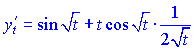
Отримані значення підставимо у формулу похідної параметричної функції 
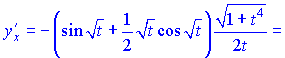
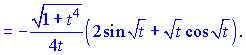
Головне у всіх прикладах не "наламати дров" при знаходженні похідних. Це найважча і відповідальна частина диференціювання параметрично заданих функцій.
4) (5.263)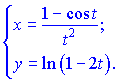 
Розв'язок. Продиференціюємо функцію та аргумент за параметром t
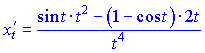
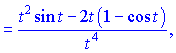
Отримані значення підставляємо у формулу і спрощуємо чисельник та знаменник на t
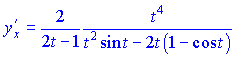
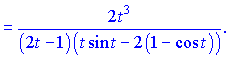
З прикладів бачимо, що обчислення похідної від параметрично заданої функції не надто складне. Дотримуйтеся послідовності виконання дій, будьте уважні при спрощенні виразів і все у Вас вийде правильно.
