На попередніх уроках детально розібрали, як знаходити похідну коли вона має вигляд суми, добутку чи частки двох функцій, що відповідає правилам (3,5,6) таблиці похідних.
Сьогодні навчимося знаходити похідні від функцій аргументом яких є функції від "ікс". Наприклад, щоб знайти похідну функції
y=(x3+x2+3x+7)5
подамо її у вигляді:
y=φ5, де φ=x3+x2+3x+7.
Тоді за формулою похідної складеної функції
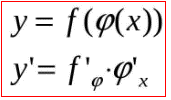(1*)
отримаємо:
y'=(φ5)'·φ'x
За формулою 8
(φ5)'=5φ4,
φ'x=(x3+x2+3x+7)'=3x2+2x+3.
Підставляємо в y':
y'=5φ4·(3x2+2x+3)=5(x3+x2+3x+7)4·(3x2+2x+3).
Формулу (1*) використовуємо для всеможливих вкладених функцій.
Приклад 1 Обчислити похідну
y=(6-7x)10.
Розв'язування: Позначимо через φ вираз в дужках
y=φ10, φ=6-7x, φ'=-7.
Тоді за правилом похідної складної функції:
y'=(φ10)'·φ'=-7·10φ9=-70(6-7x)9.
Такі обчислення під силу виконати кожному. З досвідом Ви навчитеся знаходити похідну без позначення вкладених функцій.
Приклад 2 Обчислити похідну
y=ln(3x+7).
Розв'язування: Застосовуємо формулу для логарифма (13) та правило (1*):
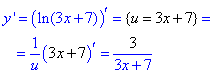
Приклад 3 Знайти похідну
y=e(x^2+4x).
Розв'язування: Показник експонетнти є функцією від "ікс", тому:
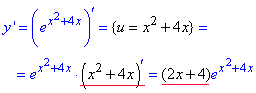
Приклад 4 Знайти першу похідну
y=√(x2+4x+3).
Розв'язування: Похідна кореня квадратного від квадратичної функції за формулами (1*,9) рівна:
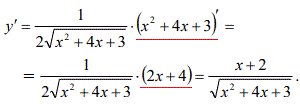
Приклад 5 Знайти похідну
y=sin(x3+5x2-1).
Розв'язування: Похідна від синуса рівна косинусу і за рахунок складеної функції домножуємо на похідну від полінома
y'=cos(x3+5x2-1)·(x3+5x2-1)'=
=(3x2+10x)cos(x3+5x2-1).
Приклад 6 Знайти похідну
y=cos5(x).
Розв'язування: Якщо задана будь-яка тригонометрична (чи будь-яка з таблиці похідних**) функція в певному степені, то за правилом похідної складеної функції за аргумент позначають саму тригонометричну (**) функцію.
y=u^5, u=cos(x).
Тоді маємо
y'=5u4·u'x=5u4·(cos(x))'=
=5cos4(x)·(-sin(x))=-5cos4(x)·sin(x).
Аналогічно похідні для тангенса та котангенса
y=tan3(x), (16)->
y'=3tan2(x)*(tan(x))'=3tan2(x)/cos2(x);
y=cot4(x), (17)->
y'=4ctg3(x)·(-1/sin2(x))=-4ctg3(x)/sin2(x).
Приклад 7 Знайти похідну
y=ctg(x4).
Розв'язування:В таких завданнях за вкладену функцію покладають
y=ctg(u), u=x4,
u'=4x3.
Обчислюємо похідну
y'=ctg(u)'·u'=-1/sin2(u)·4x3=
=-4x3/sin2(x4).
Приклад 8 Знайти похідну
y=sec2(3x).
Розв'язування: Похідну від секанса знаходимо за формулою (18)+ перед тим похідна степеневої функції
y'=2sec(3x)·(sec(3x))'=
=2sec(3x)·sec(3x)·tan(3x)*(3x)'=
=6sec2(3x)·sec(3x)·tan(3x).
Для перевірки виконаємо диференціювання в Maple:
y1 := sec(3*x)^2;
DY := diff(y1, x);
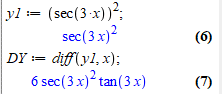
Швидко і просто.
Розглянемо кілька вложених функцій.
Приклад 9 Знайти похідну
y=tan(ln√3x).
Розв'язування: Для тангенса вкладеною функціює буде логарифм, для логарифма корінь, для кореня вкладеною ф-єю є 3х.
Тому за формулою (1*) маємо добуток похідної від тангенса на похідну від логарифма на похідну від кореня квадратного і на 3=(3х)':
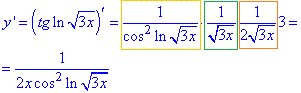
В мейплі похідна рівна:
diff(tan(ln(sqrt(3*x))),x)
В мат пакеті закладена формула переходу
1/cos2(x)=1+tg2(x).
Обчислимо ту ж похідну онлайн на wolframalpha:
Відповідь нас задовільняє.
Приклад 10 Обчислити y', якщо
y=√e2x-1.
Розв'язування: Рухаємося від кореня квадратного до експоненти далі до степеня:
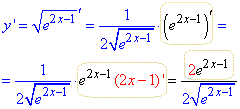
Розберемо ще завдання де маємо добуток та частку складених функцій
Приклад 11Знайти y', якщо:
y=ex^2·cos(ln(x)).
Розв'язування: За правилом похідної добутку функцій (5)
(u·v)'= похідну першої функції помножити на другу + похідну другої *на першу ф-ю.
Знайдемо спершу оремі похідні:
(ex^2)'=ex^2·(x2)'=2x·ex^2;
cos(ln(x))'=-sin(ln(x))·(ln(x))'=
= -sin(ln(x))/x.
Записуємо похідну:
y'=2x·ex^2·cos(ln(x))-ex^2·sin(ln(x))/x.
Знайдемо похідну в мат. пакеті Мейпл:
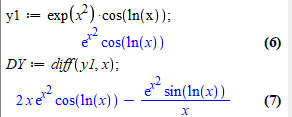
Приклад 12 Знайти похідну функції:
y=√ln(x)/etg(x).
Розв'язування: У формулі похідної частки двох функцій (6) фігурують похідні чисельника та знаменника, тому з їх обчислення і почнемо:
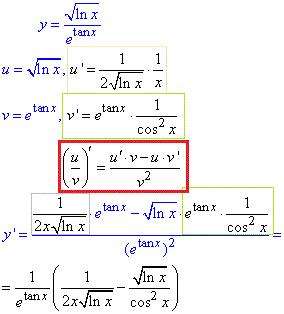
Паралельно проводимо розрахунки похідної в Maple та Wolframalpha:
y1 := sqrt(ln(x))/exp(tan(x));
DY := diff(y1, x);
З точністю до тригонометричних формул результати співпадають.
Далі вас чекають уроки на обчислення похідних неявно та параметрично заданих функцій, метод логарифмування та багато нового з диференціювання.
