Дивергенція та ротор векторного поля в точці

З уроку навчимося обчислювати дивергенцію та ротор векторного поля, дивергенцію ротора та вивчимо формули, які при цьому слід застосовувати.
Завданні не складні і левова частка розрахунків полягає в обчисленні часткових похідних. Якщо Ви добре знаєте таблицю похідних, та розв'язання подібних завдань самостійно не буде складним.

Приклад 1 Знайти дивергенцію поля a=(x•sin(x),z•ln(y),y•e^z) в точці M(π,1,0).
Розв'язання: Все що записано в поясненнях є інструкцією,що та після чого потрібно робити, щоб отримати правильну відповідь.
Першим пунктом необхідно знайти часткові похідні першого порядку поля :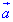

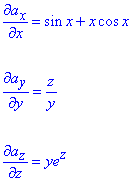
Далі обчислюємо дивергенцію поля 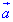за формулою:

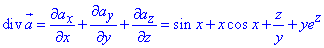
Щоб знайти дивергенцію поля в точці M(π,1,0) підставляємо координати точки в рівняння дивергенції:

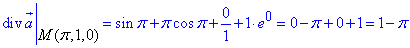
На цьому вся мудрість обчислення дивергенції закінчується.
Наведемо ще формулу ротора поля та алгоритм обчислення ротора.

Приклад 2 Знайти ротор поля 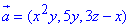в точці M(1,1,1).

Розв'язання: Випишемо проекції поля на координатні осі:
a_x=x²y, a_y=5y, a_z=3z-x.
Ротор поля a=(x²y,5y,3z-x) обчислюємо за формулою:

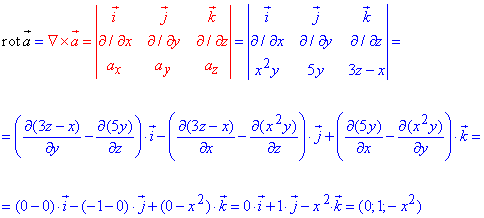
В формулі присутній визначник при розкритті якого при ортах потрібно знайти множники, які рівні різниці часткових похідних від проекцій векторного поля на осі.
Поле задане простими функціями, які легко диференціювати, тому обчислення не складні для виконання.

Ротор поля а в точці M(1,1,1) знаходимо підстановкою координат M:

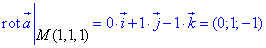
Приклад 3 Знайти дивергенцію

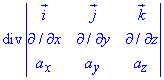
Де а(a_x,a_y,a_z) - двічі неперервно диференційовна функція.

Розв'язання: Розкриємо визначник, тобто запишемо ротор поля а(a_x,a_y,a_z):

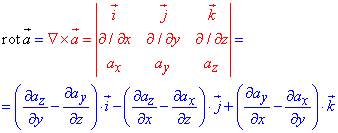
Щоб знайти дивергенцію ротора потрібно повторно диференціювати обчислені тільки що похідні за формулою: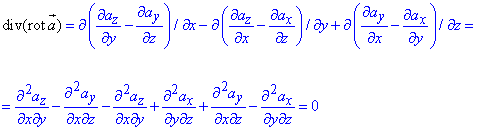
В результаті отримаємо мішані похідні другого порядку, які попарно рівні нулю та в підсумку отримуємо відому формулу:
дивергенція ротора векторного поля рівна нулю

Популярна тотожність доведена.

Приклад 4 Знайти ротор поля a=(xyz,x²+z²,x•ln(y)) в точці M(1,2,3).

Розв'язання: Записуємо проекції векторного поля на координатні осі:
a_x=xyz, a_y=x²+z², a_z=x•ln(y).

Ротор поля a=(xyz,x²+z²,x•ln(y)) знайдемо за формулою:

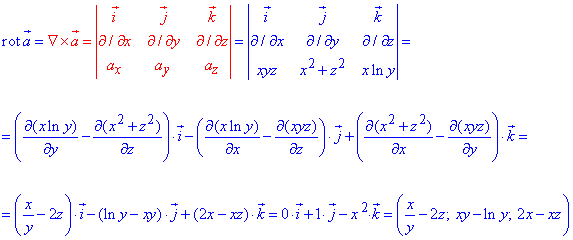
Обчислити часткові похідні від логарифма, квадратів змінних та їх добутку не важко.
Залишилося підставити в знайдене співвідношення координати M(1,2,3) та обчислити ротор поля в точці:

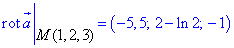
Наведені розв'язки прикладів на знаходження ротора та дивергенції поля можете використовувати на практичних, контрольних, екзаменах.
Пам'ятайте, що найкраще допомагає запам'ятати матеріал самостійна робота.
Тому побільше обчислюйте самостійно!