Второй замечательный (особый) предел часто вызывает трудности у студентов, хотя сам предел довольно прост и понятен на практике. Он позволяет раскрывать неопределенности вида единица в степени бесконечность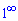 
. Замечательный предел имеет следующий вид
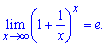
где "е"-экспонента.
Следствия второго замечательного предела
1) 
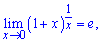
2) 
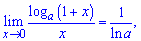
3) 
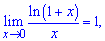
4) 
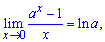
5) 
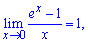
6) 
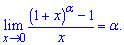
На практике следствия второго предела реже встречаются на практике чем он сам, однако без них некоторые задачи в простой способ не решить.
Примеры на замечательный предел
Рассмотрим некоторые примеры из сборника А.В. Тевяшев, А.Г. Литвин, Г.М. Кривошеева и др."Высшая математика в примерах и задачах. Ч.5 Тесты" (Харьков, 2007, ст. 99).
Пример 6.1. Найти предел функции
а)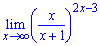 
Решение.
Преобразуем функцию к виду при котором возможно применить формулу замечательного предела
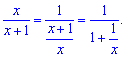
В результате можем применить правило замечательного предела
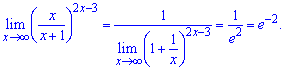
б)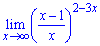
Решение.
Подобно предыдущему примеру превращаем функцию в скобках чтобы применить замечательный предел
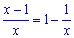
Нужно отметить, что в этом примере и во многих подобных константы в степенях, как правило вклада не несут. Функцию можно расписать следующим образом
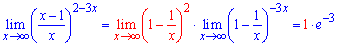
Предел умышленно расписан в виде произведения двух множителей чтобы Вы убедились что константы в степенях вклада не несут. Их цель запутать Вас, если плохо знаете теоретический материал или сомневаетесь в правильности решения. Во всех последующих примерах мы не будем расписывать примеры на произведение двух границ, однако помните, что они не меняют конечного результата (вклад - множитель единица).
------------------------------------
в)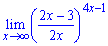 
Решение.
Выполняем преобразование заданной функции
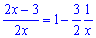
Запись в таком виде сделана специально, потому что степень нужно свести к подобному виду
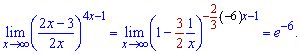
В такой простой способ получили искомый предел функции. В дальнейшем необходимые замены или подсказки будут выделены цветом из общего решения.
г)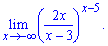 
Решение.
Выполним замену переменных в пределе
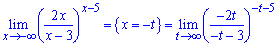
и определенные преобразования для нахождения предела
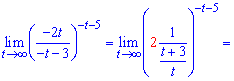
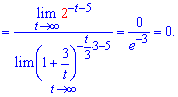
Бывают случаи, когда прямо применить правило второго замечательного предела довольно сложно, в таких ситуациях используйте простые замены которые Вам понятны и позволяют в быстрый способ найти предел.
Пример 6. 2 Вычислить предел функции
а)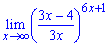 
Решение.
Сводим функцию к правилу замечательного предела
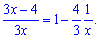
Подставляем и вычисляем, выполняя нужные манипуляции с показателями
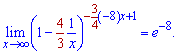
в)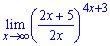 
Решение.
За известным уже алгоритмом преобразуем функцию
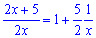
Применяя определение второго важного предела находим
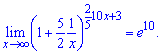
Пример 6. 3 Определить предел функции
б)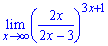 
Решение.
Сведем функцию для применения замечательного предела
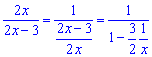
Подставляем в границу и упрощаем
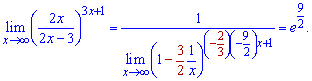
г)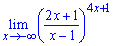 
Решение.
"Как найти предел ? - скажете Вы, ведь переменная равна минус бесконечности.
В этом примере видим что аргумент стремится к минус бесконечности, кроме того функция в скобках следует не до единицы, а до 2 при больших аргументах.
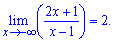
Учитывая что степень отрицательный получим следующее значение предела
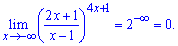
Во всех примерах второго замечательного предела следует сначала проверять условие что выражение в скобках стремится к единице. Если нет, то предел функции в зависимости от степени будет равен или нулю или бесконечности. Те из Вас кто часто решает примеры такие проверки осуществляет автоматически. Остальные сводят границу в экспоненте в определенном степени, но все равно вылезает множителем или ноль или бесконечность. В конечном варианте правы все, однако в первом случае тратится гораздо меньше времени, которое так необходима на контрольных работах, тестах, ВНО. Поэтому выбирайте для себя простой путь и делайте в обучении правильные выводы.
Пример 6. 5 Найти предел функции
а)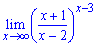 
Решение.
Заданный пример на вид отличается от предыдущих, однако решение получаем по такой же схеме. Выполняем преобразования функции в скобках под правило замечательного предела
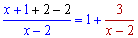
Осталось в степени выделить обратный множитель
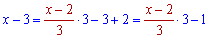
и подставить в границу
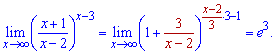
По такой схеме вычисляйте все подобные пределы, она проста и не требует дополнительных пояснений.
------------------------------------
в)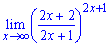 
Решение.
К рассматриваемому примеру великих преобразований делать не нужно. Он имеет достаточно простую запись и решение осуществляем в одну строку
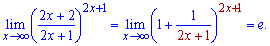
Практикуйте с подобными пределами, используйте удобные для себя схемы сведения задач под необходимое правило. Не бойтесь делать ошибки - без них обучение не обходится!
