Среди примеров пределов функции часто встречаются функции с корнями, которые не всегда понятно как раскрывать. Проще когда есть пример границе с корневой функцией вида
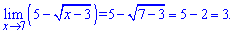
Решение подобных пределов просто и понятно каждому.
Трудности возникают если есть следующие примеры функций с корнями.
Пример 1. Вычислить предел функции
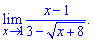
При прямой подстановке точки x = 1 видно что и числитель и знаменатель функции
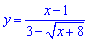
превращаются в ноль, то есть имеем неопределенность вида 0/0.
Для раскрытия неопределенности следует умножить выражение, содержащее корень на сопряженное к нему и применить правило разности квадратов. Для заданного примера преобразования будут следующими
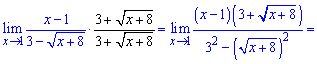
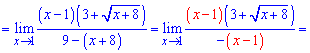
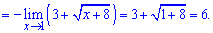
Предел функции с корнями равен 6. Без приведенного правила ее трудно было бы найти.
Рассмотрим подобные примеры вычисления границы с данным правилом
Пример 2. Найти предел функции
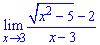
Убеждаемся что при подстановке x = 3 получаем неопределенность вида 0/0.
Ее раскрываем умножением числителя и знаменателя на сопряженное к числителю.
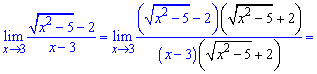
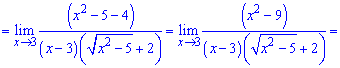
Далее числитель раскладываем согласно правилу разности квадратов
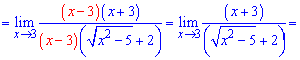
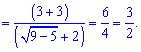
Вот так просто нашли предел функции с корнями.
Пример 3. Определить предел функции
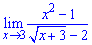
Видим, что имеем неопределенность вида 0/0.
Избавляемся ирациональносьти в знаменателе
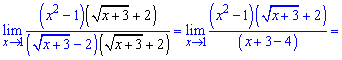
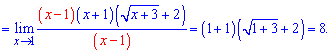
Предел функции равна 8.
Теперь рассмотрим другой тип примеров, когда переменная в переделе стремится к бесконечности.
Пример 4. Вычислить предел функции
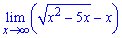
Много из Вас не знают как найти предел функции. Ниже будет раскрыта методика вычислений.
Имемем предел типа бесконечность минус бесконечность. Умножаем и делим на сопряженный множитель и используем правило разности квадратов
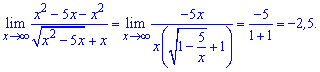
Границ функции равна -2,5.
Вычисление подобных пределов фактически сводится к раскрытию иррациональности , а затем подстановке переменной
Пример 5. Найти предел функции
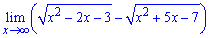
Предел эквивалентен - бесконечность минус бесконечность
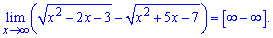 .
.
Умножим и разделим на сопряженное выражение и выполним упрощение

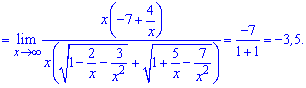
Пример 6. Чему равен предел функции?
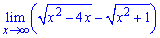
Имеем неопределенность вида бесконечность минус бесконечность
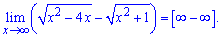
Выполняем преобразования с корневыми функциями
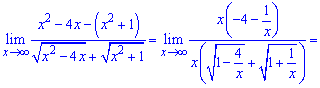
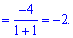
предел функции равен -2.
Хорошо ознакомьтесь с методикой раскрытия неопределенностей, алгоритм достаточно прост и поможем найти сложную границу функции.


