Смешанным произведением трех векторов 
называется число, равное векторному произведению первых двух векторов, 
, умноженному скалярно на вектор 
. Векторами это можно представить так
Так как векторы 
на практике задают в координатной форме, то их смешанный произведение равен определитель, построенном на их координатам
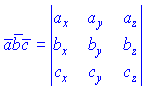
В силу того, что векторное произведение антикомутативно, а скалярное произведение коммутативно, то циклическая перестановка векторов в смешанном произведении не изменяет его значение. Перестановка двух соседних векторов меняет знак на противоположный
Смешанный произведение векторов положительный, если они образуют правую тройку и отрицательный - если левую.
Геометрические свойства смешанного произведения
1. Объем параллелепипеда, построенного на векторах 
равен модулю смешанного произведения этих векторов
2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения
3. Объем треугольной пирамиды равен одной шестой модуля смешанного произведения
4. Векторы 
планарных тогда и только тогда, когда
В координатах условие компланарности означает равенство нулю определителя
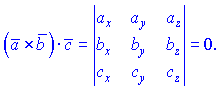
Для практического усвоения рассмотрим примеры.
-------------------------------------------
Пример 1.
Определить, какой тройкой (правой или левой) являются векторы
1)
2) 
3) 
4)
5) 
Решение.
Найдем смешанное произведение векторов и по знаку выясним, какую тройку векторов они образуют
1) 
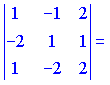
Векторы образуют правую тройку (
).
2) 
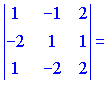
Векторы образуют правую тройку (
).
3) 
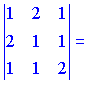
Векторы образуют левую тройку (
).
4)
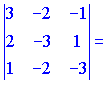
Векторы образуют правую тройку (
).
5)
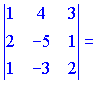
Векторы образуют левую тройку (
).
6)
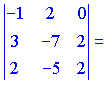
Данные векторы линейно зависимы.
-------------------------------------------
Пример 2.
Выяснить линейную зависимость векторов
1)
2)
3)
Решение.
Найдем смешанный произведение и проверим отличны от нуля определители
1) 
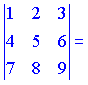
Векторы линейно зависимы (
).
2)
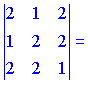
Векторы линейно независимы (
) и образуют левую тройку.
3) 
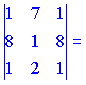
Векторы линейно зависимы (
).
Таким методом можно решить множество других задач, все в конечном итоге сводится к отысканию определителей третьего порядка. Находим определитель, анализируем его значение и принимаем нужный ответ.
----------------------------------------------
Посмотреть материалы:
