В данной статье будут изложены основные инструкции, относительно векторов. С их помощью Вы будете знать что с ними можно делать, а что нет. Поэтому переходим к изучению операций над векторами.
І. Суммой двух 
-мерных векторов
и 
называют
-мерный вектор 
, координаты которого равны сумме соответствующих координат векторов - слагаемых:
Например, если 
,
то 
Из этого правила следует, что разностью двух векторов будет вектор, координаты которого является разницей соответствующих координат векторов
ІІ. Произведением числа 
(скаляра) на 
-мерный вектор 
называется 
-мерный вектор 
, координаты которого равны произведению числа 
на соответствующие координаты вектора 
Например
Операции сложения векторов и умножения числа на вектор (
- некоторые числа) обладают свойствами:
1) 
2) 
3)
4)
5)
6)
7) Для произвольного вектора 
существует противоположный вектор 
такой, что
ІІІ. Скалярным произведением 
двух 
-мерных векторов 
и 
называют число, равное сумме произведений соответствующих координат векторов:
Например,
если
, то
Согласно другому определению, скалярное произведение двух векторов это число, равное произведению длин векторов (их модулей) на косинус угла между ними
Из приведенного выше определения можно получить формулу для вычисления угла между векторами
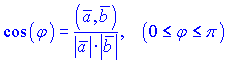
или в координатной форме
Также есть формулировка согласно которой скалярное произведение двух векторов равен модулю одного из них умноженному на проекцию второй вектор на направление первого
Из последнего определения вытекают формулы для нахождения проекции вектора на вектор
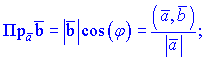
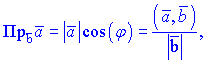
или в координатной форме
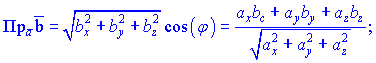
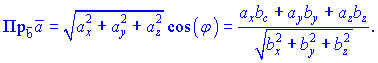
Примеры нахождения скалярного произведения, угла между векторами и проекции одного вектора на другой будут рассмотрены ниже.
Алгебраические свойства скалярного произведения векторов:
1) 
2)
3)
4)
Равенство 
имеет место при условии
Геометрические свойства скалярного произведения
1)векторы 
перпендикулярны между собой, если
2) угол между векторами 
острый в случаях, когда
3) угол между векторами 
тупой в случаях, когда
ІV. Векторным произведением 
или 
двух векторов называется вектор 
, который отвечает следующим условиям:
1) модуль вектора 
равен произведению модулей векторов 
и 
на синус угла между ними
2) вектор 
нормальный к плоскости, построенной на векторах 
и 
;
3) вектор 
направлен так, что с его конца кратчайший поворот от вектора 
к 
происходит против часовой стрелки. Иными словами, векторы 
образуют правую тройку.
Векторное произведение имеет следующие геометрические свойства:
Его модуль равен площади параллелограмма построенного на векторах 
и 
Поэтому площадь треугольника построенного на векторах 
и 
равна модулю половины векторного произведения этих векторов
Алгебраические свойства векторного произведения
1) векторное произведение 
равно нулю в случае коллинеарности векторов или когда один из них нулевой;
2) от перестановки векторов векторное произведение меняет знак на противоположный
3)
4)
На практике важно иметь под рукой формулу для вычисления векторного произведения в координатной форме, поэтому запишем и ее
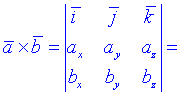
Рассмотрим конкретные примеры для усвоения пройденного материала.
--------------------------------------------
Задача 1.
Заданы векторы 
и 
Найти следующие величины
1) сумму векторов 
2) скалярное произведение векторов 
3) ) векторное произведение 
площадь треугольника построенного на векторах 
4) угол между векторами 
5) проекцию каждого из векторов на другой
Решение
1) Проведем вычисления
2) Скалярное произведение будет равно
3) Векторное произведение вычисляем по формуле
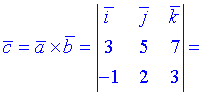
Площадь треугольника будет равна
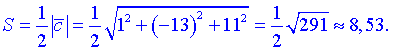
4) Найдем угол между векторами по формуле
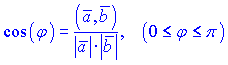
В ней скалярное произведение уже найдено поэтому находим длины векторов
Подставляем нужные значения в формулу
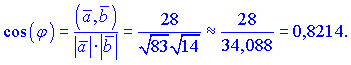
Находим значение угла
5) Найдем проекции векторов
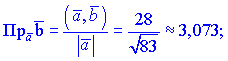
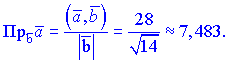
Проекции векторов можно искать через косинус угла между векторами, результат от этого не изменится
На этом урок окончен. Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.
-----------------------------------------------------
Посмотреть материалы:
