Скалярным произведением двух векторов (a, b)
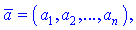
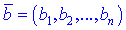
называют число равное сумме попарных произведений координат векторов с каждой оси, т.е.
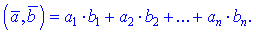
Из формулы видно что вычисление скалярного произведения - это самое простое занятие, которое может выполнить любой школьник.
Например, если есть два вектора в пространстве с координатами
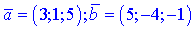
то их скалярное произведение равно 6
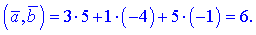
В математике есть еще одно определение скалярного произведения.
Согласно второму определению скалярное произведение двух векторов равно числу, которое получают умножением длин векторов (их модулей) на косинус угла между ними
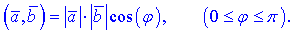
Данное определение используют не столько для нахождения скалярного произведения, как для исчисления значение косинуса угла и уже из таблиц - самого угла между векторами. Из определения получают удобную формулу для вычисления угла между векторами
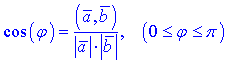
или в координатной форме
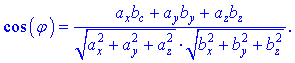
Приведем примеры вычисления скалярного произведения для трехмерных векторов.
--------------------------------------------
Примеры.
Задано векторы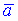 
и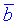 
. Вычислить их скалярное произведение, если
1) 
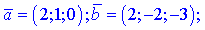
2) 
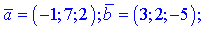
3) 
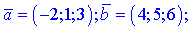
4) 
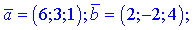
5) 
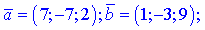
6) 
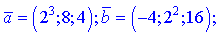
7) 
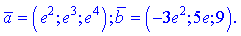
Решение. Выполним вычисления согласно формул
1) 
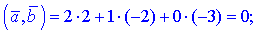
2) 
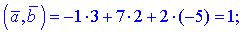
3) 
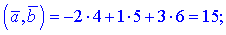
4) 
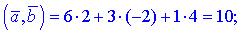
5) 
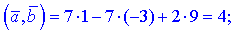
6) 
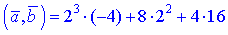
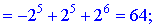
7) 
-----------------------------------
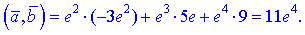
Из примеров Вы убедились, что нахождение скалярного произведения попарным перемножением координат векторов, а затем их суммированием не является сложным. В следующих статьях будут рассмотрены другие стороны скалярного произведения и его применение к векторному анализу.
Посмотреть материалы:
